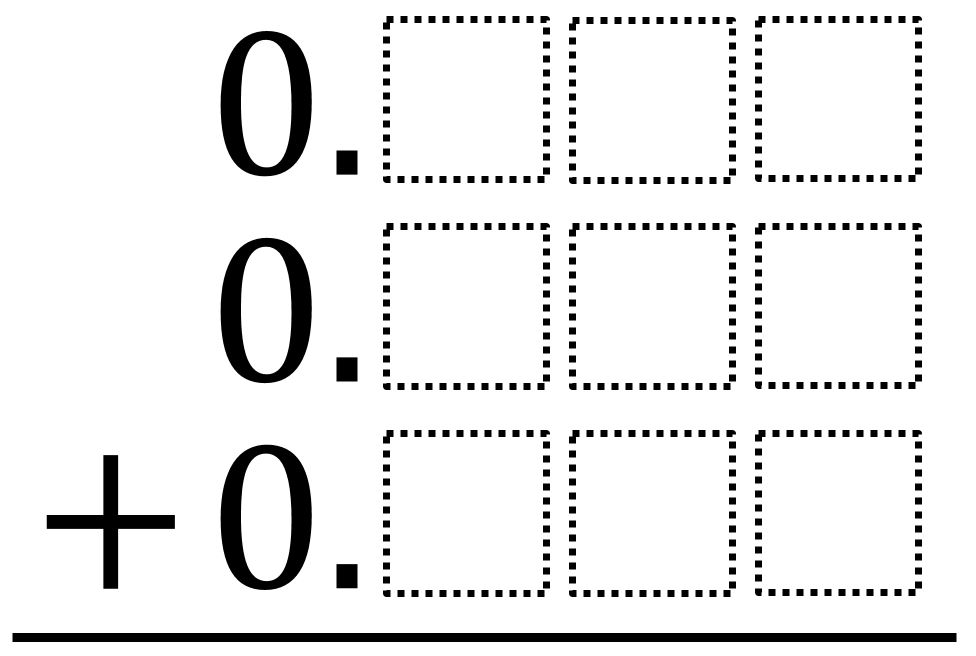
Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make three decimals whose sum is as close to 1 as possible.
Hint
How can we round each of the three decimals to quickly determine how close to one it is? How does placing a higher value number effect in each place value affect the sum?
Answer
Originally I found two sums that were equal to 0.999 but Henk Reuling made a complete list which includes: 0.125 + 0.376 + 0.498 = 0.999
0.125 + 0.378 + 0.496 = 0.999
0.125 + 0.396 + 0.478 = 0.999
0.125 + 0.398 + 0.476 = 0.999
0.126 + 0.375 + 0.498 = 0.999
0.126 + 0.378 + 0.495 = 0.999
0.126 + 0.395 + 0.478 = 0.999
0.126 + 0.398 + 0.475 = 0.999
0.128 + 0.375 + 0.496 = 0.999
0.128 + 0.376 + 0.495 = 0.999
0.128 + 0.395 + 0.476 = 0.999
0.128 + 0.396 + 0.475 = 0.999
0.134 + 0.267 + 0.598 = 0.999
0.134 + 0.268 + 0.597 = 0.999
0.134 + 0.276 + 0.589 = 0.999
0.134 + 0.279 + 0.586 = 0.999
0.134 + 0.286 + 0.579 = 0.999
0.134 + 0.289 + 0.576 = 0.999
0.134 + 0.297 + 0.568 = 0.999
0.134 + 0.298 + 0.567 = 0.999
0.136 + 0.274 + 0.589 = 0.999
0.136 + 0.279 + 0.584 = 0.999
0.136 + 0.284 + 0.579 = 0.999
0.136 + 0.289 + 0.574 = 0.999
0.137 + 0.264 + 0.598 = 0.999
0.137 + 0.268 + 0.594 = 0.999
0.137 + 0.294 + 0.568 = 0.999
0.137 + 0.298 + 0.564 = 0.999
0.138 + 0.264 + 0.597 = 0.999
0.138 + 0.267 + 0.594 = 0.999
0.138 + 0.294 + 0.567 = 0.999
0.138 + 0.297 + 0.564 = 0.999
0.139 + 0.274 + 0.586 = 0.999
0.139 + 0.276 + 0.584 = 0.999
0.139 + 0.284 + 0.576 = 0.999
0.139 + 0.286 + 0.574 = 0.999
0.143 + 0.267 + 0.589 = 0.999
0.143 + 0.269 + 0.587 = 0.999
0.143 + 0.287 + 0.569 = 0.999
0.143 + 0.289 + 0.567 = 0.999
0.147 + 0.263 + 0.589 = 0.999
0.147 + 0.269 + 0.583 = 0.999
0.147 + 0.283 + 0.569 = 0.999
0.147 + 0.289 + 0.563 = 0.999
0.149 + 0.263 + 0.587 = 0.999
0.149 + 0.267 + 0.583 = 0.999
0.149 + 0.283 + 0.567 = 0.999
0.149 + 0.287 + 0.563 = 0.999
0.152 + 0.368 + 0.479 = 0.999
0.152 + 0.369 + 0.478 = 0.999
0.152 + 0.378 + 0.469 = 0.999
0.152 + 0.379 + 0.468 = 0.999
0.158 + 0.362 + 0.479 = 0.999
0.158 + 0.369 + 0.472 = 0.999
0.158 + 0.372 + 0.469 = 0.999
0.158 + 0.379 + 0.462 = 0.999
0.159 + 0.362 + 0.478 = 0.999
0.159 + 0.368 + 0.472 = 0.999
0.159 + 0.372 + 0.468 = 0.999
0.159 + 0.378 + 0.462 = 0.999
0.162 + 0.358 + 0.479 = 0.999
0.162 + 0.359 + 0.478 = 0.999
0.162 + 0.378 + 0.459 = 0.999
0.162 + 0.379 + 0.458 = 0.999
0.163 + 0.247 + 0.589 = 0.999
0.163 + 0.249 + 0.587 = 0.999
0.163 + 0.287 + 0.549 = 0.999
0.163 + 0.289 + 0.547 = 0.999
0.164 + 0.237 + 0.598 = 0.999
0.164 + 0.238 + 0.597 = 0.999
0.164 + 0.297 + 0.538 = 0.999
0.164 + 0.298 + 0.537 = 0.999
0.167 + 0.234 + 0.598 = 0.999
0.167 + 0.238 + 0.594 = 0.999
0.167 + 0.243 + 0.589 = 0.999
0.167 + 0.249 + 0.583 = 0.999
0.167 + 0.283 + 0.549 = 0.999
0.167 + 0.289 + 0.543 = 0.999
0.167 + 0.294 + 0.538 = 0.999
0.167 + 0.298 + 0.534 = 0.999
0.168 + 0.234 + 0.597 = 0.999
0.168 + 0.237 + 0.594 = 0.999
0.168 + 0.294 + 0.537 = 0.999
0.168 + 0.297 + 0.534 = 0.999
0.168 + 0.352 + 0.479 = 0.999
0.168 + 0.359 + 0.472 = 0.999
0.168 + 0.372 + 0.459 = 0.999
0.168 + 0.379 + 0.452 = 0.999
0.169 + 0.243 + 0.587 = 0.999
0.169 + 0.247 + 0.583 = 0.999
0.169 + 0.283 + 0.547 = 0.999
0.169 + 0.287 + 0.543 = 0.999
0.169 + 0.352 + 0.478 = 0.999
0.169 + 0.358 + 0.472 = 0.999
0.169 + 0.372 + 0.458 = 0.999
0.169 + 0.378 + 0.452 = 0.999
0.172 + 0.358 + 0.469 = 0.999
0.172 + 0.359 + 0.468 = 0.999
0.172 + 0.368 + 0.459 = 0.999
0.172 + 0.369 + 0.458 = 0.999
0.174 + 0.236 + 0.589 = 0.999
0.174 + 0.239 + 0.586 = 0.999
0.174 + 0.286 + 0.539 = 0.999
0.174 + 0.289 + 0.536 = 0.999
0.175 + 0.326 + 0.498 = 0.999
0.175 + 0.328 + 0.496 = 0.999
0.175 + 0.396 + 0.428 = 0.999
0.175 + 0.398 + 0.426 = 0.999
0.176 + 0.234 + 0.589 = 0.999
0.176 + 0.239 + 0.584 = 0.999
0.176 + 0.284 + 0.539 = 0.999
0.176 + 0.289 + 0.534 = 0.999
0.176 + 0.325 + 0.498 = 0.999
0.176 + 0.328 + 0.495 = 0.999
0.176 + 0.395 + 0.428 = 0.999
0.176 + 0.398 + 0.425 = 0.999
0.178 + 0.325 + 0.496 = 0.999
0.178 + 0.326 + 0.495 = 0.999
0.178 + 0.352 + 0.469 = 0.999
0.178 + 0.359 + 0.462 = 0.999
0.178 + 0.362 + 0.459 = 0.999
0.178 + 0.369 + 0.452 = 0.999
0.178 + 0.395 + 0.426 = 0.999
0.178 + 0.396 + 0.425 = 0.999
0.179 + 0.234 + 0.586 = 0.999
0.179 + 0.236 + 0.584 = 0.999
0.179 + 0.284 + 0.536 = 0.999
0.179 + 0.286 + 0.534 = 0.999
0.179 + 0.352 + 0.468 = 0.999
0.179 + 0.358 + 0.462 = 0.999
0.179 + 0.362 + 0.458 = 0.999
0.179 + 0.368 + 0.452 = 0.999
0.183 + 0.247 + 0.569 = 0.999
0.183 + 0.249 + 0.567 = 0.999
0.183 + 0.267 + 0.549 = 0.999
0.183 + 0.269 + 0.547 = 0.999
0.184 + 0.236 + 0.579 = 0.999
0.184 + 0.239 + 0.576 = 0.999
0.184 + 0.276 + 0.539 = 0.999
0.184 + 0.279 + 0.536 = 0.999
0.186 + 0.234 + 0.579 = 0.999
0.186 + 0.239 + 0.574 = 0.999
0.186 + 0.274 + 0.539 = 0.999
0.186 + 0.279 + 0.534 = 0.999
0.187 + 0.243 + 0.569 = 0.999
0.187 + 0.249 + 0.563 = 0.999
0.187 + 0.263 + 0.549 = 0.999
0.187 + 0.269 + 0.543 = 0.999
0.189 + 0.234 + 0.576 = 0.999
0.189 + 0.236 + 0.574 = 0.999
0.189 + 0.243 + 0.567 = 0.999
0.189 + 0.247 + 0.563 = 0.999
0.189 + 0.263 + 0.547 = 0.999
0.189 + 0.267 + 0.543 = 0.999
0.189 + 0.274 + 0.536 = 0.999
0.189 + 0.276 + 0.534 = 0.999
0.194 + 0.237 + 0.568 = 0.999
0.194 + 0.238 + 0.567 = 0.999
0.194 + 0.267 + 0.538 = 0.999
0.194 + 0.268 + 0.537 = 0.999
0.195 + 0.326 + 0.478 = 0.999
0.195 + 0.328 + 0.476 = 0.999
0.195 + 0.376 + 0.428 = 0.999
0.195 + 0.378 + 0.426 = 0.999
0.196 + 0.325 + 0.478 = 0.999
0.196 + 0.328 + 0.475 = 0.999
0.196 + 0.375 + 0.428 = 0.999
0.196 + 0.378 + 0.425 = 0.999
0.197 + 0.234 + 0.568 = 0.999
0.197 + 0.238 + 0.564 = 0.999
0.197 + 0.264 + 0.538 = 0.999
0.197 + 0.268 + 0.534 = 0.999
0.198 + 0.234 + 0.567 = 0.999
0.198 + 0.237 + 0.564 = 0.999
0.198 + 0.264 + 0.537 = 0.999
0.198 + 0.267 + 0.534 = 0.999
0.198 + 0.325 + 0.476 = 0.999
0.198 + 0.326 + 0.475 = 0.999
0.198 + 0.375 + 0.426 = 0.999
0.198 + 0.376 + 0.425 = 0.999
0.125 + 0.378 + 0.496 = 0.999
0.125 + 0.396 + 0.478 = 0.999
0.125 + 0.398 + 0.476 = 0.999
0.126 + 0.375 + 0.498 = 0.999
0.126 + 0.378 + 0.495 = 0.999
0.126 + 0.395 + 0.478 = 0.999
0.126 + 0.398 + 0.475 = 0.999
0.128 + 0.375 + 0.496 = 0.999
0.128 + 0.376 + 0.495 = 0.999
0.128 + 0.395 + 0.476 = 0.999
0.128 + 0.396 + 0.475 = 0.999
0.134 + 0.267 + 0.598 = 0.999
0.134 + 0.268 + 0.597 = 0.999
0.134 + 0.276 + 0.589 = 0.999
0.134 + 0.279 + 0.586 = 0.999
0.134 + 0.286 + 0.579 = 0.999
0.134 + 0.289 + 0.576 = 0.999
0.134 + 0.297 + 0.568 = 0.999
0.134 + 0.298 + 0.567 = 0.999
0.136 + 0.274 + 0.589 = 0.999
0.136 + 0.279 + 0.584 = 0.999
0.136 + 0.284 + 0.579 = 0.999
0.136 + 0.289 + 0.574 = 0.999
0.137 + 0.264 + 0.598 = 0.999
0.137 + 0.268 + 0.594 = 0.999
0.137 + 0.294 + 0.568 = 0.999
0.137 + 0.298 + 0.564 = 0.999
0.138 + 0.264 + 0.597 = 0.999
0.138 + 0.267 + 0.594 = 0.999
0.138 + 0.294 + 0.567 = 0.999
0.138 + 0.297 + 0.564 = 0.999
0.139 + 0.274 + 0.586 = 0.999
0.139 + 0.276 + 0.584 = 0.999
0.139 + 0.284 + 0.576 = 0.999
0.139 + 0.286 + 0.574 = 0.999
0.143 + 0.267 + 0.589 = 0.999
0.143 + 0.269 + 0.587 = 0.999
0.143 + 0.287 + 0.569 = 0.999
0.143 + 0.289 + 0.567 = 0.999
0.147 + 0.263 + 0.589 = 0.999
0.147 + 0.269 + 0.583 = 0.999
0.147 + 0.283 + 0.569 = 0.999
0.147 + 0.289 + 0.563 = 0.999
0.149 + 0.263 + 0.587 = 0.999
0.149 + 0.267 + 0.583 = 0.999
0.149 + 0.283 + 0.567 = 0.999
0.149 + 0.287 + 0.563 = 0.999
0.152 + 0.368 + 0.479 = 0.999
0.152 + 0.369 + 0.478 = 0.999
0.152 + 0.378 + 0.469 = 0.999
0.152 + 0.379 + 0.468 = 0.999
0.158 + 0.362 + 0.479 = 0.999
0.158 + 0.369 + 0.472 = 0.999
0.158 + 0.372 + 0.469 = 0.999
0.158 + 0.379 + 0.462 = 0.999
0.159 + 0.362 + 0.478 = 0.999
0.159 + 0.368 + 0.472 = 0.999
0.159 + 0.372 + 0.468 = 0.999
0.159 + 0.378 + 0.462 = 0.999
0.162 + 0.358 + 0.479 = 0.999
0.162 + 0.359 + 0.478 = 0.999
0.162 + 0.378 + 0.459 = 0.999
0.162 + 0.379 + 0.458 = 0.999
0.163 + 0.247 + 0.589 = 0.999
0.163 + 0.249 + 0.587 = 0.999
0.163 + 0.287 + 0.549 = 0.999
0.163 + 0.289 + 0.547 = 0.999
0.164 + 0.237 + 0.598 = 0.999
0.164 + 0.238 + 0.597 = 0.999
0.164 + 0.297 + 0.538 = 0.999
0.164 + 0.298 + 0.537 = 0.999
0.167 + 0.234 + 0.598 = 0.999
0.167 + 0.238 + 0.594 = 0.999
0.167 + 0.243 + 0.589 = 0.999
0.167 + 0.249 + 0.583 = 0.999
0.167 + 0.283 + 0.549 = 0.999
0.167 + 0.289 + 0.543 = 0.999
0.167 + 0.294 + 0.538 = 0.999
0.167 + 0.298 + 0.534 = 0.999
0.168 + 0.234 + 0.597 = 0.999
0.168 + 0.237 + 0.594 = 0.999
0.168 + 0.294 + 0.537 = 0.999
0.168 + 0.297 + 0.534 = 0.999
0.168 + 0.352 + 0.479 = 0.999
0.168 + 0.359 + 0.472 = 0.999
0.168 + 0.372 + 0.459 = 0.999
0.168 + 0.379 + 0.452 = 0.999
0.169 + 0.243 + 0.587 = 0.999
0.169 + 0.247 + 0.583 = 0.999
0.169 + 0.283 + 0.547 = 0.999
0.169 + 0.287 + 0.543 = 0.999
0.169 + 0.352 + 0.478 = 0.999
0.169 + 0.358 + 0.472 = 0.999
0.169 + 0.372 + 0.458 = 0.999
0.169 + 0.378 + 0.452 = 0.999
0.172 + 0.358 + 0.469 = 0.999
0.172 + 0.359 + 0.468 = 0.999
0.172 + 0.368 + 0.459 = 0.999
0.172 + 0.369 + 0.458 = 0.999
0.174 + 0.236 + 0.589 = 0.999
0.174 + 0.239 + 0.586 = 0.999
0.174 + 0.286 + 0.539 = 0.999
0.174 + 0.289 + 0.536 = 0.999
0.175 + 0.326 + 0.498 = 0.999
0.175 + 0.328 + 0.496 = 0.999
0.175 + 0.396 + 0.428 = 0.999
0.175 + 0.398 + 0.426 = 0.999
0.176 + 0.234 + 0.589 = 0.999
0.176 + 0.239 + 0.584 = 0.999
0.176 + 0.284 + 0.539 = 0.999
0.176 + 0.289 + 0.534 = 0.999
0.176 + 0.325 + 0.498 = 0.999
0.176 + 0.328 + 0.495 = 0.999
0.176 + 0.395 + 0.428 = 0.999
0.176 + 0.398 + 0.425 = 0.999
0.178 + 0.325 + 0.496 = 0.999
0.178 + 0.326 + 0.495 = 0.999
0.178 + 0.352 + 0.469 = 0.999
0.178 + 0.359 + 0.462 = 0.999
0.178 + 0.362 + 0.459 = 0.999
0.178 + 0.369 + 0.452 = 0.999
0.178 + 0.395 + 0.426 = 0.999
0.178 + 0.396 + 0.425 = 0.999
0.179 + 0.234 + 0.586 = 0.999
0.179 + 0.236 + 0.584 = 0.999
0.179 + 0.284 + 0.536 = 0.999
0.179 + 0.286 + 0.534 = 0.999
0.179 + 0.352 + 0.468 = 0.999
0.179 + 0.358 + 0.462 = 0.999
0.179 + 0.362 + 0.458 = 0.999
0.179 + 0.368 + 0.452 = 0.999
0.183 + 0.247 + 0.569 = 0.999
0.183 + 0.249 + 0.567 = 0.999
0.183 + 0.267 + 0.549 = 0.999
0.183 + 0.269 + 0.547 = 0.999
0.184 + 0.236 + 0.579 = 0.999
0.184 + 0.239 + 0.576 = 0.999
0.184 + 0.276 + 0.539 = 0.999
0.184 + 0.279 + 0.536 = 0.999
0.186 + 0.234 + 0.579 = 0.999
0.186 + 0.239 + 0.574 = 0.999
0.186 + 0.274 + 0.539 = 0.999
0.186 + 0.279 + 0.534 = 0.999
0.187 + 0.243 + 0.569 = 0.999
0.187 + 0.249 + 0.563 = 0.999
0.187 + 0.263 + 0.549 = 0.999
0.187 + 0.269 + 0.543 = 0.999
0.189 + 0.234 + 0.576 = 0.999
0.189 + 0.236 + 0.574 = 0.999
0.189 + 0.243 + 0.567 = 0.999
0.189 + 0.247 + 0.563 = 0.999
0.189 + 0.263 + 0.547 = 0.999
0.189 + 0.267 + 0.543 = 0.999
0.189 + 0.274 + 0.536 = 0.999
0.189 + 0.276 + 0.534 = 0.999
0.194 + 0.237 + 0.568 = 0.999
0.194 + 0.238 + 0.567 = 0.999
0.194 + 0.267 + 0.538 = 0.999
0.194 + 0.268 + 0.537 = 0.999
0.195 + 0.326 + 0.478 = 0.999
0.195 + 0.328 + 0.476 = 0.999
0.195 + 0.376 + 0.428 = 0.999
0.195 + 0.378 + 0.426 = 0.999
0.196 + 0.325 + 0.478 = 0.999
0.196 + 0.328 + 0.475 = 0.999
0.196 + 0.375 + 0.428 = 0.999
0.196 + 0.378 + 0.425 = 0.999
0.197 + 0.234 + 0.568 = 0.999
0.197 + 0.238 + 0.564 = 0.999
0.197 + 0.264 + 0.538 = 0.999
0.197 + 0.268 + 0.534 = 0.999
0.198 + 0.234 + 0.567 = 0.999
0.198 + 0.237 + 0.564 = 0.999
0.198 + 0.264 + 0.537 = 0.999
0.198 + 0.267 + 0.534 = 0.999
0.198 + 0.325 + 0.476 = 0.999
0.198 + 0.326 + 0.475 = 0.999
0.198 + 0.375 + 0.426 = 0.999
0.198 + 0.376 + 0.425 = 0.999
Notes
To make this problem fit nicely on a web page, I have placed the three decimals above one another. The downside of doing this is that it encourages students to go directly to using the standard algorithm. So, if you are doing this with students, I would suggest putting the decimals side by side. Also, the idea behind absolute value may come up during the lesson. Specifically, is 0.997 (a difference of -0.003) closer to 1 than 1.002 (a difference of 0.002). Also note that this problem can be modified to being decimals to the hundredth to make it appropriate for 5th grade.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Our 6th graders came up with three more solutions for 0.999:
0.139 + 0.576 + 0.284; 0.458 + 0.369 + 0.172; 0.597 + 0.268 + 0.134
Awesome work! We appreciate their work and solutions. They have been added to the solution set.
😀
Just do 987+654+321
I had a student who came up with 0.176 + 0.234 + 0.589
Thank you for finding another solution, we added it to the page.
Habe die Vorlesung mittlerweile komplett angeschaut und kann nur sagen, dass sie ziemlich gut und verständlich ist. Manchmal schlägt natürlich der professorale Elfenbeinturm der Wissenschaft durch (RSA erklären als Party-Highlight?!), aber mit etwas Mitdenken bekommt man wirklich viel vermittelt.Eine Katastrophe ist allerdings die Mitarbeit der Studenten/innen, die alle samt die Vorlesung im Dämmerzustand verbringen und vermutlich nie eine der Ãœbungen absolviert haben – wirklich schade.
Hello,
I have seen 6th graders work on this problem today. It is such a rich task, kudos to the open middle team!
What I liked the most was our discussion around “being close to zero” does not necessarily mean your number has to be less than 1. Then we started looking for numbers that are in same distance from 1. It was a really good experience.
One caveat though; some students use random numbers without a strategy and get lucky. Teachers have to pay more attention to the strategies students use (and modify).
I’m so excited to try this with my students! Thank you Open Middle team for all of the inspiring ideas!
.149+.283+.657=1.089
close but more than 1
.175 + .326 + .498
I did 0.333+0.333+0.333=0.999. I then did 0.462+0.318+0.220=1.000. for my last one I did 0.465+0.318+0.220=1.000. this problem was a little difficult to wrap my head around and when I did it was so easy.
Hi Brian. I think you might need to re-read the instruction as it says “use the numbers 1 through 9, exactly one time each.” Unfortunately your attempts use the same numbers more than one time each.
Actually he doesnt use the numbers twice you probably got confused but we can repeat the numbers IN THE ANSWER but not in the boxes so this IS ACTUALLY RIGHT so you are wrong. Sorry
He repeated the 2 in .220
0.543 +0.267 +0.189
0.398+0.426 +0.175= 0.999
A fourth grader found this one: 0.289+0.163+0.547 = 0.999
i got
0.164
0.297
0.538
i got
0.164
0.297
+0.538
I just got… 0.187 + 0.269 + 0.543 = 0.999
I am using it tomorrow with my class. I can’t wait to see what they come up with : )
0.125+0.376+0.498
Our Fifth Graders came up with:
0.147+0.283+0.569=0.999 and 0.594+0.267+0.138=0.999
I am wondering why the decimal numbers are arranged vertically (line up the decimals!). The grade 5 standard is “Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.” (5.NBT.7) This description would seem to point students to use base ten blocks, diagrams such as open number lines and arrays, and composition and decomposition (think Kathy Richardson) to solve an addition problem such as this with conceptual understanding.
Could it be rewritten in a horizontal format to move students away from procedural number crunching?
Andrew that’s an interesting thought and could lead to students choosing their own method for solving/ checking their computation. If you are trying to break students out of the traditional addition algorithm (trading/ carrying) then lining it up horizontally could be helpful. The students then choose the best way to arrange the tiles for them. Although it doesn’t look quite as pretty as a 3×3 grid…
Hi Andrew and Bob. I appreciate your point. I think it simply came down to fitting better on a page. If you try it using another layout, I’d love to hear about how it turns out.
.569 + .287 + .143 = .999
I keep sets of 0-9 or 1-9 number tiles at the ready, which can make it easier for students to try different strategies at a quicker pace, although this could potentially lead to more random guessing. I got them to go along with Marcy Cook’s Tile Teaser type problems, which are also great learning tools
Bob, great call. Yeah, I still have my Marcy Cook soft tiles and use them all the time with these kinds of problems.
This was a very interesting puzzle. On the first try I found out that one could do 1.008 following the rules, on the second try I got the correct answer which was 999 and using the same answer I managed to get 9 correct answers in a row. This was sent from Alex, 9yo
A sixth grader at ASD found the following solution today: 0.243+0.189+0.567= 0.999
My solution was 0.379 + 0.158 + 0.462 = 0.999. My reasoning was that the numbers added up from top to bottom had to come close to 9 or 19, and if the right column was going to carry a 1, then the next column left should add up to 8, not 9, or 18, not 19. Only the first/left column needed to add up to a single digit number close to 9 but no greater.
Neat. I haven’t heard anyone share that strategy before. I think I used more of a guess and check approach which changed to careful switching of numbers as I got closer to 1.
that’s exactly what I did too, Mary, and came up with 0.589+0.267+0.143, which I haven’t seen anyone post.
Great question/activity. We tried as close to 1 as possible on either side. We got 0.999 a number of ways but tried to get as close to 1 greater but greater than one and came up with 1.008 as the closest. We are trying to figure out why (or if) we should be able to get to 1.001 if we can get to 0.999 – both equidistant from 1.000
Yeah, that is surprisingly difficult to prove. I believe (but am not certain) that you can get 1.004. Proving that exactly 1 is not possible (or that 1.001 is not possible) is not something I’ve figured out how to do except via brute force of trying every possibility using a computer.
This is easier if we think of writing three 3-digit whole numbers whose sum is close to 1000 (because I find it easier to talk about whole numbers than tenths, hundredths, and thousandths). If we write the numbers as ABC, DEF, and GHI, then their values are actually 100A+10B+C, 100D+10E+F, and 100G+10H+I. Changing the structure of these expressions, we get 99A+9B+(A+B+C), etc. Putting them all together, we end up with:
99A+9B+(A+B+C) + 99D+9E+(D+E+F) + 99G+9H+(G+H+I), or
(99A+9B+99D+9E+99G+9H)+(A+B+C+D+E+F+G+H+I),
which is the sum of all nine digits plus a multiple of 9. Since the sum of the nine digits is 45, which is another multiple of 9, this means that any three 3-digit numbers we might write (with distinct nonzero digits) will always add up to a multiple of 9. 1000 isn’t a multiple of 9, so it isn’t possible to reach. The two numbers nearest 1000 that we might hope to reach are 999 and 1008.
In the original problem, this means 1.000 is impossible to reach. This also means that if we go over 1, the best we can hope to do is 1.008.
This is really cool. I proved to myself you can’t get exactly 1 by a combination of logic and brute force, but I like your way much better!
Thanks for your comment. If you want more information about similar things, try searching on:
* Casting out nines
* Digital root
* Arithmetic modulo 9
A faster way of saying the most important stuff in my earlier remark would be:
“Modulo 9, ABC + DEF + GHI is congruent to A+B+C+…+I = 45, which is congruent to 0. Therefore ABC + DEF + GHI is a multiple of 9.”
It’s almost magically efficient, but I didn’t write it initially because I thought it was a little out of bounds, not being in the Common Core. It’s an accessible and beautiful part of number theory, and I would consider it for enrichment for students who’ve met math content standard 4.NBT.6.
Is that you, Brad Ballinger, from HSU? I was just headed in this direction with a proof, but you beat me to it. 🙂 You were an inspiration for me during college and I’m now teaching high school math.
What!? Yes, I’m that guy! How we run into each other the first time I visit this site is beyond me. Email me–my email address hasn’t changed, but I’m guessing yours has? We have some catching up to do.
one of my friends was holding back on showing this to the public but he now gave me permission to show this to the public he said “the way to make 1 with 3 decimal numbers using 1-9 without repeating numbers is 0.604+0.137+0.259=1.00”
The one thing about this solution is that it used the digit 0, which is not listed in the directions for the problem. By adding the digit zero as an option, it does open the possibility of an “exactly 1” solution.
My students came up with .569 +.287+.143; .469+.378+.152
0.583 + 0.269 + 0.147= 0.999
I got 0.147+0.263+0.589=.999
I did this problem with my 7th graders and it too toke them numerous tries. A encouraged a few that did not get 0.999 to try to see if they could get closer to 1. Some aimed to get over 1, but close to 1. As you stated in your answer….the closest is .999. Classes enjoyed this open-ended question. I gave out a problem of yours on complementary and supplementary today. Use the numbers 0-9 to place in the boxes to get a complementary and a supplementary situation. The two classes that I gave it to also enjoyed the open-endedness of this question. All were able to solve it with various answers. I think there were 6 different solutions. Thank you very much for these wonderful problems. They encourage my students to have more confidence in their math abilities.
When I did this problem, my class and I had numerous ways to get to .999. But as I pondered about it as the day went on, I found out that there is no possible way to get to a sum of 1. My rationale is that the right column should add up to 20, the middle column should equal 18, and the left column should be equal to 8. This is true, because if you add the problem entirely, you will get a sum of 0 in the right column and then carry a 2 to the middle column. If the middle column is equal to 18, and then you carry the 2 over, it also sums up to 20. Then, you carry the 2 to the left column. If the left column had equaled 8 it would then become 10 because of the 2 that was carried over. Then, the final sum would be 1.000. This is not true, because 20+18+8= 46. But, 1+2+3+4+5+6+7+8+9= 45. Therefore, there is no possible solution to getting a sum of 1, by using digits 1-9 exactly once as decimals that have three-digits.
.478+.369+.152 add up to .999 and if you turn the problem 90 degrees clockwise and add the new horizontal 3 digit numbers it still equals .999.
In most of our answers, the tenths places can be interchanged with each other, as can the hundredths and thousandths places.
0.136 + 0.584 + 0.279 is one that I don’t see up there
0.462 + 0.359 + 0.178 = 0.999
It would be interesting to prompt a discussion with higher-level classes about what makes a solution “unique” in this case.
For instance, 0.462+0.359+0.178 versus 0.458+0.372+0.169. If the same three numbers are still in any given place value, are the solutions really “different?”
I have observed that in every solution of 0.999 the digits in the tenths column add up to 8, the digits in the hundredths column add up to 18, and the digits in the thousandths column add up to 19. So, finding different combinations of three digits that add up to 8, 18, and 19 will give you a plethora of solutions since the digits 1-9 add up to 45.
To get a solution of exactly 1.000 you would need to have the digits in the tenths column add up to 8, the digits in the hundredths column add up to 19, and the digits in the thousandths column add up to 10, but 8+19+10=37 so it is impossible to get these column sums because all of these digits 1-9 add up to 45. The other possibility would be if the digits in the tenths column add up to 8, the digits in the hundredths column add up to 18, and the digits in the thousandths column add up to 19, but 8+18+19=46 which is 1 greater than 45, so it is impossible to get these column sums as well since the digits 1-9 only add up to 45.
Any combination of:
Tenths: (1,2,5)
Hundredths: (3,7,8)
Thousandths: (4,6,9) Ex: 0.134 + 0.276 + 0.589
Tenths: (1,2,5)
Hundredths: (4,6,8)
Thousandths: (3,7,9) Ex: 0.143 + 0.267 + 0.589
Tenths: (1,3,4)
Hundredths: (5,6,7)
Thousandths: (2,8,9) Ex: 0.152 + 0.368 + 0.479
Tenths: (1,3,4)
Hundredths: (2,7,9)
Thousandths: (5,6,8) Ex: 0.125 + 0.376 + 0.498
0.134 + 0.276 + 0.589 this is one solution I don’t believe has been shared above
I challenged a group of fifth graders with this problem, and they worked on and off all day. Eight of them were able to find a solution that equaled 0.999 most of which have already been shared above. They talked about their brains being tired, but “good tired!” This was a great example of productive struggle and the importance of perseverance.
0.198 + 0.376 + 0.425 = 0.999 and 0.125 + 0.376 + 0.498 = 0.999
Wow. Thanks for giving me the answers to this particular problem! It was kind of hard and I didn’t want to take the time to do it myself. Thanks y’all!
0.521+0.238+0.240=0.999
.333
.333
.334
Interestingly, you can’t get a sum of 1.001 (or 1.002 to 1.007, so there wouldn’t be a discussion whether 1.002 is closer to 1 than 9.98 as suggested in the Notes section). So the 180 solutions that result in 0.999 really are the best solutions.
If we modify the task such that each of the three decimal numbers only has two digits after the decimal point (as suggested in the Notes section), we get that the following 24 solutions equal to 1 exactly:
0.13 + 0.28 + 0.59
0.13 + 0.29 + 0.58
0.14 + 0.27 + 0.59
0.14 + 0.29 + 0.57
0.15 + 0.36 + 0.49
0.15 + 0.37 + 0.48
0.15 + 0.38 + 0.47
0.15 + 0.39 + 0.46
0.16 + 0.35 + 0.49
0.16 + 0.39 + 0.45
0.17 + 0.24 + 0.59
0.17 + 0.29 + 0.54
0.17 + 0.35 + 0.48
0.17 + 0.38 + 0.45
0.18 + 0.23 + 0.59
0.18 + 0.29 + 0.53
0.18 + 0.35 + 0.47
0.18 + 0.37 + 0.45
0.19 + 0.23 + 0.58
0.19 + 0.24 + 0.57
0.19 + 0.27 + 0.54
0.19 + 0.28 + 0.53
0.19 + 0.35 + 0.46
0.19 + 0.36 + 0.45
this is pretty difficult I do not know what to do