Directions: Using the digits 1 to 9 at most one time each, place a digit in each box to make a solution that is as close to 100 as possible.
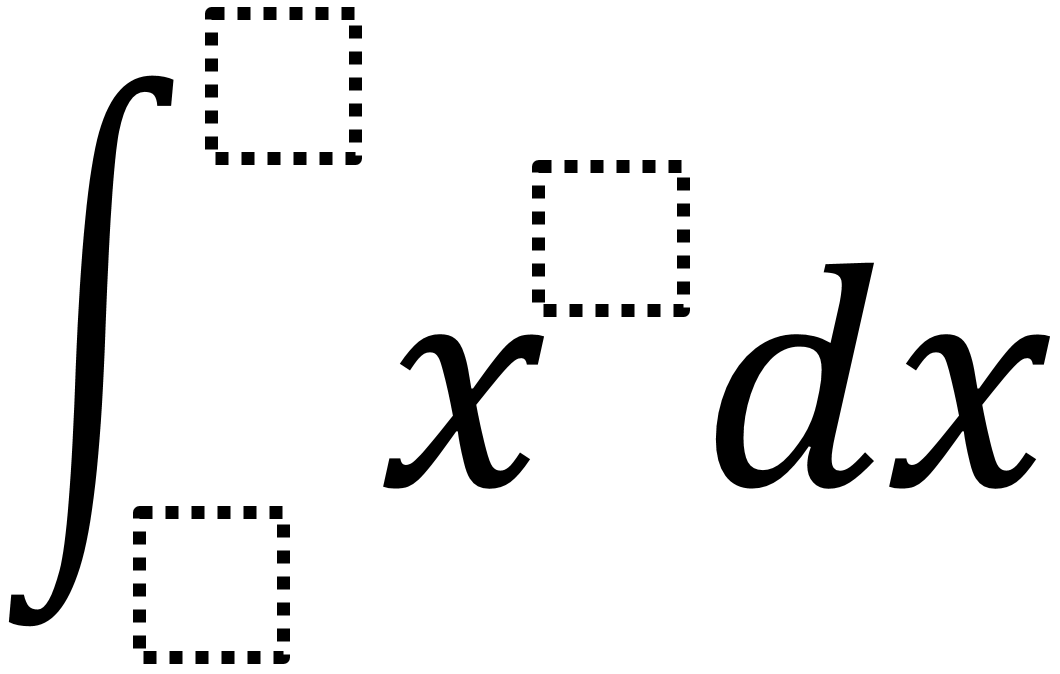
Hint
How do the upper and lower bounds determine whether the solution is negative or positive?
Answer
I only know how to figure this out via brute force and would love to learn if anyone has a conceptual approach to this.
I created this spreadsheet and tried all 9 potential exponent values. The bounds and exponent that result in a value as close to 100 as possible are:
upper bound: 8
lower bound: 6
exponent: 2
value: 98.666…
and a close second place is:
upper bound: 2
lower bound: 1
exponent: 9
value: 102.30
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



I created a desmos graph to quickly sift through solutions. I integrated leaving the exponent as a variable, and then used “x” and “y” to be the upper and lower bound and set the whole thing equal to 100. I used the slider to change the exponent “c”, and then found solutions for x and y where x is not equal to y and the points are approximately integral. I came up with exponent 2, upper bound 8, lower bound 6; exponent 3, upper bound 5, lower bound 4; and exponent 9, upper bound 2, lower bound 1. The optimal solution is exponent 2, which is 98.6666666…
Here is the desmos graph I used: https://goo.gl/QEc25d
This is really cool Alison! I had never thought about it visually. I’ll need to think about this more.
One of my students did the integral from 0 to 2.9 for x^5. She wondered if she could use it since the problem didn’t restrict them to integers. 😉
I guess that could work, but by “digit” it was intended to be an integer. Creative thinking though!
I think there’s always going to be some casework to this problem, but this is how I did it by hand. I think given some time to puzzle over this question, it’s fair for a motivated calculus student to come up with this or a similar approach.
Expressing the integral from “a” to “b” of x^n leads to (b^(n+1) – a^(n+1))/(n+1) = 100, or as close to it as possible. So, for example, if n=4, you’re looking for b^5-a^5 to be as close to 500 as possible.
Using this logic, you can eliminate many possibilities based on the fact that consecutive terms of the sequence {x^n} are going to separate more and more as we increase n. For example, the terms of {x^5} = {1, 32, 243, 3125, …} are more “spread out” than those of {x^4} = {1, 16, 81, 256, 625, 2401, …}. The {x^4} sequence contains 256 and 625, whose difference is a bit near 400, but no other pair is close, and the {x^5} sequence has no differences close to 500. For n=6, we can consider the first three terms: {x^6} = {1, 64, 729,…} and see that 729 – 64 is significantly larger than 600 to realize that we only have to think about a = 1 and b = 2 for n > 6. It’s important to watch these cases, though, because 2^10 – 1^10 = 1023 is pretty close to 1000, leading to 102.3, which is the second-best answer.
Note that n = 1 is not worth considering because that would require two perfect squares being near 200 apart when the largest square we’re considering is 81.
Finally, this leads to n = 2, and looking for perfect cubes of digits that are about 300 apart. Examining {x^3} = {1, 8, 27, 64, 125, 216, 343, 512, 729}, we notice 216 and 512, which ends up yielding the best result of 296/3 = 98.333… for the integral.
Though I have to say that the Desmos slider approach mentioned by Alison above is very cool, and would apply to a wider audience of students. With math competition students, they will know lots of squares, cubes, etc. and be able to do this problem without a calculator. I have also started to use Desmos and sliders, including animations, more and more often in my calculus classes, though, and I think these visual demos really draw in a lot of students. Thanks for sharing!