Directions: Make the largest (or smallest) expression by using the digits 0-9, no more than one time each, in the boxes below. Note: for 5th grade, remove the exponent to make it grade level appropriate.
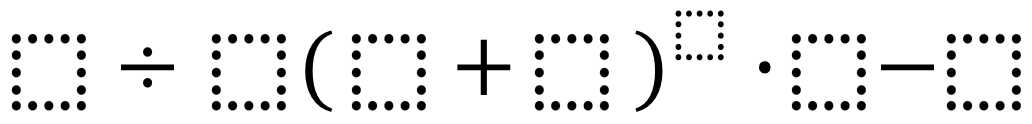
Hint
How can we tell where it would be best to put the larger/smaller numbers?
Answer
Largest: 6 ÷ 1 (8 + 7)^9 · 5 – 0 = 1,153,300,781,250
Smallest: If the answer can be positive or negative, then putting a 0 in the first term and a 9 in the last term makes it -9. If the answer must be positive, then 5 ÷ 9 (4 + 7)^0 · 2 – 1 = 1/9.
Source: Robert Kaplinsky with answer from Michael Fenton and his students.
 Open Middle®
Open Middle®



I must be missing something. My students got about 1.15 trillion, and I agree with them. I think it comes down to interpretation of the second operation (reading left to right).
Here are three options, two of which must be equivalent: https://www.evernote.com/shard/s5/sh/9d33a64c-f44b-415c-b505-921434224ad9/c6ad61b74f22237bbb7cd894b12d4c07/deep/0/MathType—Untitled-3.png
My vote? Option (C) is the odd one out.
If I’m wrong, can someone help me understand why?
I feel like B is the odd one out. When I see a(b), I see this as “a” “b’s”, making it equivalent to option C. I’m not sure why I think this and I can’t find anything to back up my logic. I feel like a similar conversation was had a few years ago on Twitter and someone (Cox) concluded that either could be correct but that, to avoid ambiguity, parentheses should be used.
I agree with option C being the odd one out. In option A you are going to follow up parenthesis and exponents with multiplying and dividing left to right. This means that you would divide 6 by 1 next which is the same thing you do next in option B since it is in parenthesis. In option C you are going to multiply by 1 before dividing 6 by a really big number! That’s going to give you a very small answer.
To me, a/b(c-d)
implies a/[b(c-d)], whereas a/b*(c-d)
implies (a/b)(c-d).
Again, I have looked and can’t find anything to back up my logic…
I think that Option C is the most interesting. I’m changing the problem to a/[b(c+d)] so the kids have to make the denominator as small as possible
So there is some logic to C. In fact, when there is implied multiplication like a/b(c-d) then for some there is some ambiguity as to what is meant. Personally I don’t think there is but the Internet and calculators say otherwise. I posted this (https://twitter.com/davidpetro314/status/908082923856953345) a few weeks ago on Twitter and found that when the multiplication is implied. On some calculators, this multiplication takes precedence (see the discussion that followed my post). Apparently this is an advanced feature. We don’t typically teach this in elementary or HS but apparently many engineers are aware of this “extra” order of operations rule. I have found very little about this but I did see one small reference to the fact that it has to do with b being a scale factor when in the form b(c-d) (http://blogs.ptc.com/2011/11/10/math-basics-order-of-operations-precedence-and-tricky-brainteasers/). I’m not sure I 100% agree but it is definitely a thing (especially when calculators have it as explicit rules https://twitter.com/MrBinfield/status/908367572634099713)
There are other exceptions to PEMDAS dogma. For example, consider the number -1 1/2. (If I could typeset that better, it would properly look like “negative one and a half”.) Before you read any further, please plot that number on a number line.
The negative sign in front is implicit multiplication, whereas the “and a half” part is implicit addition. If we evaluate the multiplication first, then the number ends up between -1 and 0; but if you’re like me, you put it between -1 and -2, which is consistent with evaluating implicit addition before implicit multiplication.
The order of operations is an agreement between people in order to ease communication. PEMDAS seeks to abbreviate that agreement, but it oversimplifies some parts.
I think that as long as we can debate whether A means B or C, the conclusion is that whoever wrote A didn’t write it clearly enough. Instead of rating readers on the basis of how well they guess the mind of the author, we should send the expression back for further editing.
thank you i am a student witch had to do this problem thx for the awnser
Ah, I think you are right and that the answer I listed is wrong. I meant for it to be C but it turned out to be B. Nice catch! I will update the answer accordingly.
Just as David Meyer explained, C IS the odd one out. The order of operations is very clear that, when you have just multiplication and division, you do them in the order written. That makes A and B the same problem; B is just more clearly delineated.
I have been teaching algebra for 25 years; my husband (who also checked this problem) has a master’s in Mathematics and a PhD in Math Education.
Doesn’t the smallest possible (positive) answer have the same interpretation issue? (BTW: When I copy and paste 1 ÷ 6 (7 + 8)^9 · 2 into Wolfram Alpha I get an answer on the order of 1.28 x 10^10.)
Again, nice catch Gale. Thanks for the feedback. I tried it again and the smallest positive answer I was able to get is 1/4. Anyone have a better one?
Nanette just got 1/9 so I replaced my solution with hers.
4/8 (9+7)^0 x2-1
I believe this equals 0
Great problem and easy to adapt! Just wanted to share what I’m planning to do for an intro to Exponential Rules (more of a review) in Algebra!
I think I’m going to use just the binomial raised to the power and try to max/min it using only 1-3. Brings up a good discussion hopefully about when we can distribute the exponent and when we can’t! I might also adapt it for our other exponential rules 🙂
Yay open middle!
Side though, loving using just negative integers too!!!
Thanks Katrine. That’s a great idea. Please submit that as a problem of its own!
For working on this with kids I’m less interested in the right answer but in the reasoning and conversations about how to approach and what are the things to consider in placing the numbers. I’m happy with a really big answer and a really small answer and the reasoning. Although some will continue to find the smallest and largest and that’s lovely too
type this into the online Google calendar and you get 30 instead of the large number. Excel only return a large number if you change the formula to include a * before the parenthesis.
Where does it say that numbers can’t be re-used? I got just over 16 trillion, using a lot of 9’s. I’m going to try this problem with my 6th graders today and see what they get. I may include the rule that they can only use each number once, and then also see what the smallest positive number is that they can get. Fun problem! Great practice for students once they get the basics of the Order of Operations!
That’s a really great point Chris. I guess you could use numbers more than once with the way it is written. That being said, using all 9s or even a lot of 9’s could be very bad for making an expression with the greatest value as you have to divide by much of it.
The answer should be 9/1(9+9)^9 · 9-0
9/0(9+9)^9 · 9-0 while not a specific answer, doesn’t this approach infinity? thereby being the largest possible answer?
Sorry, strangely I did not write “no more than one time each” and have added that. But yes, you would be right without that restriction.
What would the answer be if you removed the exponent for 5th grade?
My students arrived at 810 with either 9 / 1 ( 8 + 7 ) * 6 – 0 or with the 9 and 6 switched.
For grade 5 without the exponent, I think the largest result is 9/1(6+7)x8 – 0 (or swap the 8 and 9). I would use the division sign instead of / to save confusion about whether (6+7) is part of the denominator (which is not what’s meant) or the numerator (which it is).
I would explain this algebraically (not to 5th grade) as:
a / 1 (b + c) x d -0 = a(b+ c) x d = (ab + ac) x d = abd + acd then, because a and d occur in both terms, replace them by the largest possible possible (it doesn’t matter which is the larger number). The 1 and the 0 don’t really affect the answer
Can’t the 5 and 6 be switched in the solution for the largest number?
My students arrived at 810 with either 9 / 1 ( 8 + 7 ) * 6 – 0 or with the 9 and 6 switched.
The correct answer is A (or B). You mustn’t insert extra brackets as it changes the answer in many cases. * The Mathematical rule says to do the brackets which are there first. * Then do Multiplication and division working from left to right (just like reading words) * then finish off doing any addition and subtraction, again working from left to right. * If there is no operation sign (e.g. between the 1 and (8+7) a mathematician assumes it is 1x(8+7).In algebra, we omit the multiplication sign when there is no ambiguity as it can be confused with the pronumeral (letter) ‘x’. * Since a power is more “powerful” than a product (e.g. 2^9 = 512, but 2 x 9 is only 18), 9 should be the power to get the maximum answer. * The 5 and the 6 could have been interchanged in this instance because of the associative law e.g. 2 x 3 x 4 is the same as 4 x 3 x 2 or 3 x 2 x 4 etc. and division by 1 leaves the first number unchanged.
Now, for the minimum number:the 6 or the 5 should be replaced by 0 (anything x 0 = 0). The 0 should be replaced by 9, giving an answer of -9. Avoid division by 0 as this does produce infinity (or an answer which is undefined in the real number system. The other numbers don’t matter.
This is a great question to generate discussion. I would stipulate no repeat digits at the start of the discussion.
That’s enough for now.
If you take out the exponents, does anyone know what the answer would be?
This was a great task for my students today. I gave them the restriction of digits 1-9 instead of 0-9. First goal was create the largest number, next task was create the smallest number, third extension was add a set of brackets to create the smallest number (thereby giving them the opportunity to subtract at the end for a negative number to multiply by). Lots of thinking, reasoning, and math conversation!
The answer depends on if the implicit multiplication by juxtaposition between ▢(▢+▢)^▢ is supposed to take precedence over the division right before. Nowadays, ▢÷▢(▢+▢)^▢ would most often be interpreted as ▢÷▢*(▢+▢)^▢=(▢÷▢)*(▢+▢)^▢, because division and multiplication have the same priority, so it’s evaluated from left to right. I’m going to go forward assuming implicit multiplication by juxtaposition doesn’t have higher priority than explicit multiplication or division.
Smallest possible result is 0 ÷ 1 * (2 + 3)^4 * 5 – 9 = -9
Greatest possible result is 5 ÷ 1 * (7 + 8)^9 * 6 – 0 = 1,153,3007,812,250 (you can swap the 5 and the 6 or the 7 and 8 for the same result)
If we remove the exponent to make it appropiate for 5th grade:
Smallest possible result is 0 ÷ 1 * (2 + 3) * 4 – 9 = -9
Greatest possible result is 9 ÷ 1 * (7 + 6) * 8 – 0 = 936
If the intention was to have the implicit multiplication have priority over the division (I’ve added brackets to make it more clear), then the answers are:
Smallest possible result is 0 ÷ (1 * (2 + 3)^4) * 5 – 9 = -9
Greatest possible result is 9 ÷ (1 * (7 + 3)^0) * 8 – 2 = 70
If we remove the exponent to make it appropiate for 5th grade:
Smallest possible result is 0 ÷ (1 * (2 + 3)) * 4 – 9 = -9
Greatest possible result is 8 ÷ (1 * (0 + 2)) * 9 – 3 = 33