Directions: Use the digits 1 to 9, at most one time each, to make three equivalent fractions.
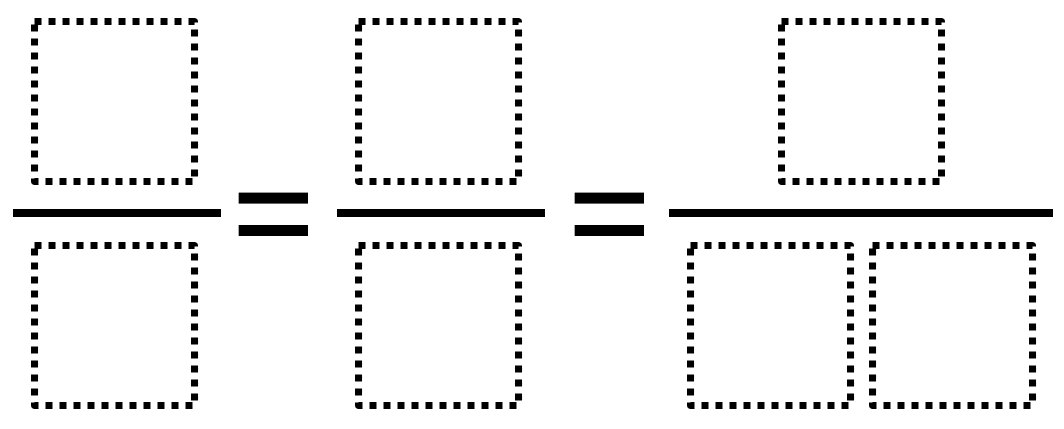
Hint
What must be true about all three fractions?
Answer
There are three possibilities:
6/8 = 3/4 = 9/12
2/4 = 3/6 = 9/18
2/8 = 1/4 = 9/36
6/8 = 3/4 = 9/12
2/4 = 3/6 = 9/18
2/8 = 1/4 = 9/36
Source: Owen Kaplinsky
 Open Middle®
Open Middle®



As far as my class could figure out the answers you present are the only three possibilities. We worked on creating organized lists to rule out all other possibilities.
When you start with the simplified version of the fraction:
-no numerators or denominators greater than 4 will work because when you multiply them by 2 they become a two digit number and we need two fractions with single digit denominators (i.e. 2/5 x 2= 4/10 two digit numerator – 2/6, x 2 = 4/12 – etc)
-The only possibilities for most simplified fraction to begin with are 1/2, 1/3, 1/4, 2/3, 3/4 – and 1/3 and 2/3 do not work
– 1/2: use 2/4, 3/6, 9/18
-1/3 doesn’t work
-1/4: 1/4, 2/8, 9/36
-2/3 – doesn’t work
-3/4: 3/4, 6/8, 9/12
Thanks. Just updated it.
2/5 x 2 = 4/5 not 4/10.
2/6 x 2 = 4/6 not 4/12
Third grade can use
1/2, 3/6,4/8
I am curious why this task is tagged with Common Core 3.NF since Grade 3’s expectation in NF are limited to fractions with denominators of 2, 3, 4, 6, and 8. Would this task be better suited for Grade 4 where students work with denominators of 2, 3, 4, 5, 6, 8, 10, and 12?
Agree….I’ll use it for 4th grade. It’s a great one for that grade level.
Good point. I changed it.
That could work, but I think it is fine. Thanks for your opinion!
1/2=3/6=4/8
J/k, I overlooked the second blank 🙂
im not understanding how we are supposed to show are kids how to do this work with out any examples or any understanding on how to do this
2/6=3/1=4/12
3/1 is not = 2/6 and 4/12
I think they meant 1/3, not 3/1…but either way the 1 cannot be used since it appears in the 12.
500000/1000000=1/2=300/600
5/10=2/4=1/2
4/8=3/6=1/2
I have the name Owen too!
The 10 has a zero which isn’t in the 1 to 9 realm
2/4=3/6=9/18
If you allow the option of the digit zero, there are two more possibilities:
2/4 = 3/6 = 5/10
4/8 = 3/6 = 5/10
In fact, why not allow the possibility of zero? It’s important that students begin thinking about it? Is that too much for a 4th grader to deal with in fractions? (I have no idea–I teach high school.)
I was thinking that might have made it too easy, since most students know the fractions equivalent to 1/2 already. Not having the 0 makes them have to calculate lesser used equivalent fractions. That being said, I’m having my students discuss the use of 0 and how it changes the possible combinations as a follow-up to the activity!
2/4 = 4/8 = 5/10
This uses 4 twice, and doesn’t follow the given instructions of using only the digits 1-9. Other than that, it’s a true math sentence.
the answers 2/4=4/8-5/10
Minh? what u doin
Real bro. Aren’t you supposed to be asleep rn?
Who the hell are you? why would i be asleep im a teacher why would i be asleep t 9:20.