Directions: Using the digits 1 to 9 at most one time each, place a digit in each box to create a quadratic equation with the greatest possible maximum value.
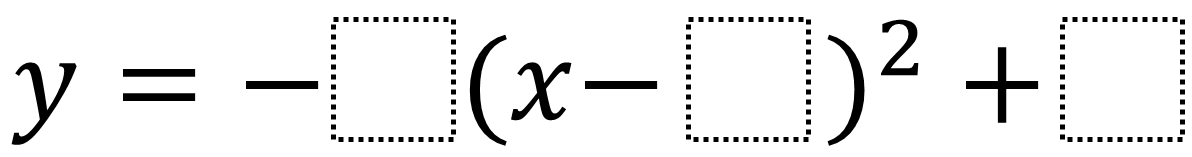
Hint
Where is the best place to put the 9? How does each box affect the graph’s behavior?
Answer
There are many solutions but a 9 must go into the last term as the k-value. That affects its y-axis position while the the a and h terms affect its width and x-axis position. Play with the sliders on this Desmos graph for a hands on way of understanding how the a, x, and k terms affect the quadratic: https://www.desmos.com/calculator/uffgbapfzf
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



What makes this problem a DOK 3? It seems too simple to be a DOK 3. Please help me understand. Thank you.
Hi Karen. I’m not going to win an award for a speedy response, but the reason it’s a DOK 3 is the optimization. It’s challenging enough to make a quadratic that (as an example) goes through a given point. However, to find the absolute maximum value requires much deeper understanding.
I understand what Karen is saying. The constant at the end is the value that affects the maximum. So it must be 9. The other two numbers can be anything as the number in the parentheses affects the horizontal shift, and the constant in front of the parentheses affects how wide or narrow the parabola is. Unless you are allowing multiple digits in each box? As long as you know how each number affects the shape or location of the parabola, this is not too difficult a question.