Directions: Using the digits 1- 9, at most one time each, to fill in the boxes to make each expression evaluate to a perfect square number.
Extension/Challenge: What is the largest/smallest square number you can make? How many different perfect square numbers could be made?
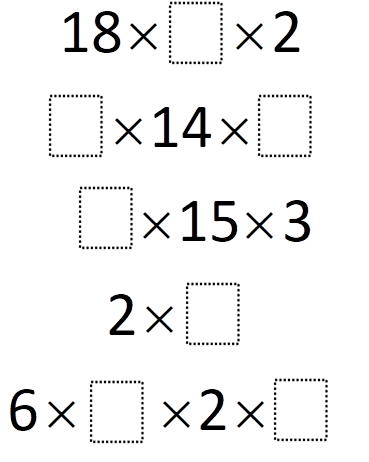
Hint
Answer
Number of Unique Solutions: 12
#1:
18 x 1 x 2 = 36
2 x 14 x 7 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 3 x 2 x 9 = 324
#2:
18 x 1 x 2 = 36
7 x 14 x 2 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 3 x 2 x 4 = 144
#3:
18 x 1 x 2 = 36
7 x 14 x 8 = 784
5 x 15 x 3 = 225
2 x 2 = 4
6 x 3 x 2 x 9 = 324
#4:
18 x 1 x 2 = 36
8 x 14 x 7 = 784
5 x 15 x 3 = 225
2 x 2 = 4
6 x 4 x 2 x 3 = 144
#5:
18 x 4 x 2 = 144
7 x 14 x 2 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 3 x 2 x 1 = 36
#6:
18 x 4 x 2 = 144
7 x 14 x 2 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 9 x 2 x 3 = 324
#7:
18 x 4 x 2 = 144
7 x 14 x 8 = 784
5 x 15 x 3 = 225
2 x 2 = 4
6 x 3 x 2 x 1 = 36
#8:
18 x 4 x 2 = 144
8 x 14 x 7 = 784
5 x 15 x 3 = 225
2 x 2 = 4
6 x 9 x 2 x 3 = 324
#9:
18 x 9 x 2 = 324
7 x 14 x 2 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 3 x 2 x 1 = 36
#10:
18 x 9 x 2 = 324
7 x 14 x 2 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 4 x 2 x 3 = 144
#11:
18 x 9 x 2 = 324
7 x 14 x 8 = 784
5 x 15 x 3 = 225
2 x 2 = 4
6 x 3 x 2 x 1 = 36
#12:
18 x 9 x 2 = 324
7 x 14 x 8 = 784
5 x 15 x 3 = 225
2 x 2 = 4
6 x 3 x 2 x 4 = 144
Source: Erick Lee
 Open Middle®
Open Middle®



18 x 4 x 2 = 144
2 x 14 x 7 = 196
5 x 15 x 3 = 225
2 x 8 = 16
6 x 1 x 2 x 3 = 36
I used factors of the given numbers and then matched them up to make sure that there were two of each which would make them perfect squares.
Thanks for sharing your solution Robert – I’ve added it to the other answers 🙂
explain further
That was a good solution