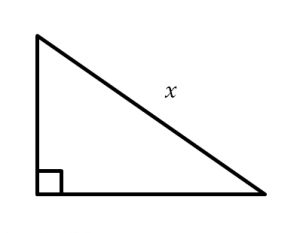
Directions: What could the lengths of the legs be such that the lengths are integers and x is an irrational number between 5 and 7?
Hint
What is a wrong answer? How can you use this wrong answer to move towards an answer?
What does it mean to be irrational between 5 and 7?
Answer
Here are the lengths of the legs
3 and 5,
3 and 6,
4 and 4,
4 and 5,
2 and 5,
2 and 6,
1 and 5,
1 and 6
3 and 5,
3 and 6,
4 and 4,
4 and 5,
2 and 5,
2 and 6,
1 and 5,
1 and 6
Source: Daniel Luevanos
 Open Middle®
Open Middle®



I said 3 and 4
Which Pair is it??
Can someone help me out with how 6 and 2 & 6 and 1 are solutions?
6^2 + 2^2 = 36 + 4 = 40. The sqrt of 40 is not an irrational number (it ends) = 6.32455532.
Also, 6^2 + 1^2 = 36 + 1 = 37. The sqrt of 37 is not an irrational number = 6.08276253.
Both numbers end, therefore are not irrational.
Just because the decimal ends on your calculator does not mean that it actually ends. The calculator will only show a certain number of digits on your screen.
Sqrt(40) is irrational because 40 is not a perfect square. The decimal places will keep going and will never repeat a sequence, so therefore it is irrational.
Only perfect squares are rational. sqrt(25) = 5
A calculator provides a rounded decimal because it must. It would not be possible to list the infinite number of digits for irrational numbers, so it must be approximated when represented in decimal form.