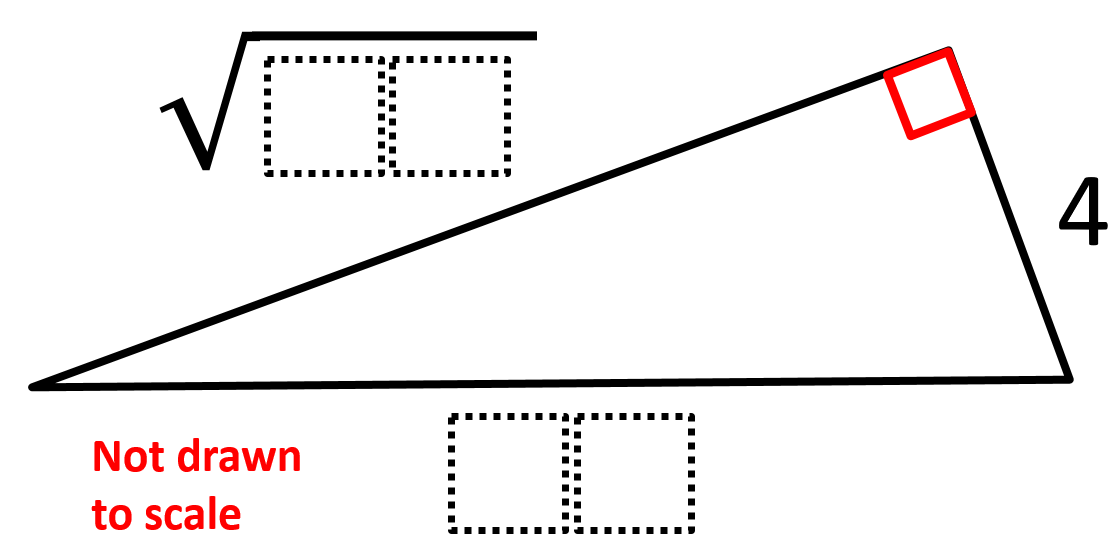
Directions: Using the digits 0 to 9, at most one time each, fill in the boxes to find two pairs of possible lengths for the missing sides.
Hint
How do we figure out which side length would be easiest to assume?
How do we figure out the length of the remaining side?
How do we figure out the length of the remaining side?
Answer
The longest possible length for the hypotenuse is 10. If it was 11, you would not be able to make the leg long enough and only two digits. It also can’t be 4 or less as the hypotenuse has to be the longest side.
So, the possible side lengths for the triangles are (a, b, and c being the leg, leg, and hypotenuse):
a, b, c
4, √84, 10
4, √65, 09
4, √48, 08
4, √33, 07
4, √20, 06
4, 03, 05
After removing the solutions that duplicate digits, you are left with only two options:
a, b, c
4, √65, 09 (from Suzie)
4, √84, 10
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



A solution that is missing from your list: 4, sqrt(65), 9 (because 16 + 65 = 81)
I also don’t know how 4, 3, 5 could be an answer because assuming that the two adjacent boxes mean that it needs to be a 2-digit number, you would need to use “05” and “09” in the boxes to make it work. That repeats the 0 digit more than once.
You are totally right, Suzie. I’ve updated the answer accordingly.
The 4, 03, and 05 answer is incorrect. Because the 03 is in the radical, it would need to be 09 in order for it to be a 3-4-5 triangle
__
4, V65, 09
Sorry it meant to be:
__
4, V65, 09