Directions: Using the digits 1 to 9, at most one time each, fill in the boxes to make the following expression as close to 0 as possible.
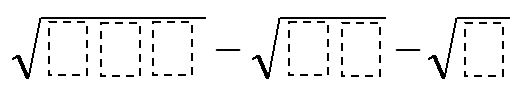
Hint
What are all the perfect square three digit numbers? Several of these can’t be used since they contain a repeated digit (e.g. 121 uses the digit 1 twice and 144 uses the digit 4 twice)
Answer
Using Perfect squares:
Sqrt(256) – sqrt(81) – sqrt(9) = 4
Sqrt(256) – sqrt(81) – sqrt(9) = 4
Using non-perfect squares:
Sqrt(145) – sqrt(92) – sqrt(6) = 0.00044178938368
Source: Erick Lee
 Open Middle®
Open Middle®



Dang it.
I got:
√124 – √89 – √3 = -0.030503214
You tried. That is what is important!
Good job!! It doesn’t matter if you make a mistake! The important thing is that you tried! You did your personal best and that is what matters!!! Just keep trying and you will make a good answer eventually!! Just do your personal best and if you get it wrong than don’t worry about it! it is fine! Keep on trying!
The 4 closest answers are 138, 95, 4
124 69 8
132 75 8
145 92 6
But 124 69 8 is the most epik because 69
Should it not be √256 – √81 -√49 = 0 ?
Your answer looks correct. Maybe the wording needs to be clarified? It says as close to zero, maybe the question needs to state without equaling zero?
The last term has space for only one digit, so √49 doesn’t work.
I thought there could only be one digit square root on the last term?
Correct Kathy and Suzanne. Unfortunately Kristen, the last root must have a single digit.
256-81-9=4
The answer should be
√121-√81-√4
The answer to this equation would be 0
You can only use the digit “1” at most once.
or 11-9-2 when It is simplified
or √121-√64-√9
The answer would be 0 as well
you are repeating the number 1 , 121 has two and then theres a third “1” in 81
/121-/64-/9=0
257-81-49=4
|256|-|81|-/9/=4
|121|-|81|-|4|
|121|-|81|-|5|
|121|-|82|-|5|
121-81-9= 4
I was working on this problem in preparation for having my 8th grade students work on it. I assumed that I should place digits so that the digits under each radical formed a perfect square, but then I realized the directions didn’t explicitly state that. I am interested in hearing how teachers have used this problem in their classroom and the discussions that resulted.
So far I have √105 – √68 – √4 = .00073951472
Update: I got √140 – √9 – √78 = 0.00039869987
These are great answers! I always wonder with the open middle problems allowing 1-9, why not 0-9? Sometimes I can see how it makes a big difference in the problem. Other times, like this one, it just seems to me that the answers with a 0 are better.
answer: sqrt169-sqrt81-sqrt4=2
om’s answer was 4
and 2<4
sooooooooo
I hope it’s right