Open Middle®
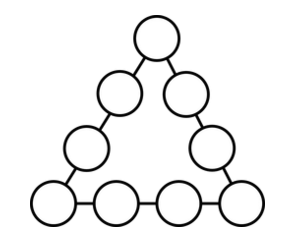
Instrucciones: Escribe dentro de cada círculo uno de los dígitos del 1 al 9, sin repetir, de manera que, siendo la suma de los círculos de cada lado la medida correspondiente a ese lado, se forme el triángulo con el mayor (o menor) ángulo posible.
Sugerencias
¡Ten cuidado de no hacer triángulos imposibles! Recuerda que el teorema de la desigualdad del triángulo dice que la suma de dos lados siempre es mayor al otro lado.
El menor ángulo interior del triángulo es siempre opuesto al lado menor.
El mayor ángulo interior del triángulo es siempre opuesto al lado mayor.
Repuesta
El mayor ángulo posible es 150.799º. Existen varias formas de acomdar los números para lograrlo. Un ejemplo es: Lado A: 6+8+9+7=30 Lado B: 7+4+1+3=15 Lado C: 3+2+5+6=16 Ángulo A: 150.799 Ángulo B: 14.119 Ángulo C = 15.082. Un posible triángulo con el menor ángulo que se puede formar es: Lado A: 1+2+3+4=10 Lado B: 4+8+9+7=28 Lado C: 1+5+6+7=19 Ángulo A: 10.844 Ángulo B: 148.212 Ángulo C = 20.944
Origen: Erick Lee
