Open Middle®
Directions: Fill in the blanks with integers so that the quadratic expression is factorable.
Hint
Answer
2. 11, -11, 4, -4, 1, -1
3. 25, -25, 14, -14, 11, -11, 10, -10
4. 1, -5, -2, -9, …this goes on and on. Can you find a pattern?
Use Algebra tiles to see this physically. I found it to be easier if I used Algebra Tiles, especially with the last problem, which, by the way, has more than a couple answers.
By the way, I usually teach factoring with Algebra Tiles.
Here is how I set up Algebra Tiles. When you use tiles to factor, you are trying to arrrange the tiles into a rectangle (think area model).
First, I grab the necessary tiles.
Then, I arrange the yellow tiles into a rectangle.
All (big blue square and rectangle of yellow small unit squares) of the pieces will make a rectangle, with missing chunks, the missing chunks represent the missing b term in the quadratic.
Then, fill in the missing chunks with the skinny (green, means positive) rectangles, representing x.
Then, fill in the missing chunks with the skinny (red, means negative) rectangles, representing x.
You can now go back to the first picture and see if there are any more possible rectangles that can be arranged with the yellow pieces.
By the way, this get trickier if the pieces are negative. Enjoy!
Source: Nanette Johnson
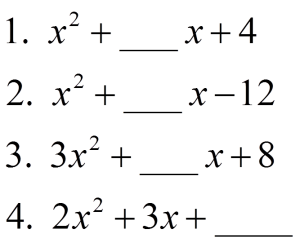
1. x² + 4x + 4
2. x² + 4x – 12
3. 3x² + 14x + 8
4. 2x² + 3x – 2
1. 5
2. -11
3. 25
4. -2
I may be missing something obvious, but I don’t understand what the hint (“Give me a number that you know does not work. How can you prove that it does not work? …) is getting at.
A different hint that comes to my mind is, “If the polynomial (with the missing number filled in) is factorable, what must the factors look like?”
For example, for problem 3, the factors would have to have the forms x+p and 3x+q for some integers p and q. (Or maybe they could be -x+p and -3x+q, but that won’t lead to any more possibilities for the missing coefficient when all is said and done. [Why?]) So the product will be
(x+p)(3x+q) = 3x² + (3p+q)x + pq .
Now all we have to do is enumerate the choices of p and q the will give the correct constant coefficient pq = 8, and for each choice the missing linear coefficient will be 3p+q. So the possibilities are:
p = 8; q = 1; 3p+q = 25
p = 4; q = 2; 3p+q = 14
p = 2; q = 4; 3p+q = 10
p = 1; q = 8; 3p+q = 11
p = -1; q = -8; 3p + q = -11
etc.
For problem 4, the factors will have the forms x+p and 2x+q, with product
(x+p)(2x+q) = 2x² + (2p+q)x + pq .
We can get the correct linear coefficient by picking integers p and q such that 2p+q = 3, and the missing constant term will then be the product pq. But the equation 2p+q = 3 is satisfied precisely by letting p be any integer and letting q be 3-2p. So the values for the missing constant term in 2x² + 3x + __ that give a factorable polynomial are integers of the form
pq = p(3-2p) = 3p-2p²
for any integer p.
The only possible non-negative values for 3p-2p² are 0 (when p = 0) and 1 (when p = 1) [Why?]. There are infinitely many negative possibilities, some arising from integers p ≤ -1 and others from integers p ≥ 2.