Directions: Using the digits 1 to 9, at most one time each, create an equation where x has the smallest (or greatest) possible value.
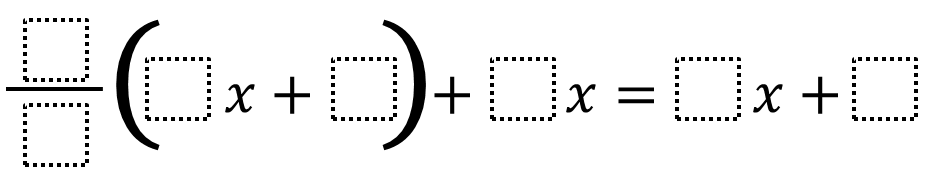
Hint
Where do you want to put the smaller (or larger) numbers?
How does choosing the coefficient or constant affect the variable’s value?
How does choosing the coefficient or constant affect the variable’s value?
Answer
The smallest solution I’ve found so far is x = -70
(9/1)(3x + 8) + 4x = 6x + 2
(9/1)(3x + 8) + 4x = 6x + 2
The largest solution I’ve found so far is x = 8:
(4/8)(6x + 2) + 1x = 3x + 9
Source: Daniel Luevanos
 Open Middle®
Open Middle®



Here is an equation where x=20.
(9/3)(1x+8)+2x=6x+4
The smallest solution I found x = -2.8
(9)(3x + 8) + 4x = 6x + 2
27x + 72 + 4x = 6x + 2
31x +72 = 6x + 2
25x + 72 = 2
25x = -70/25
x = -2.8
Here is an equation where x=61
(1/7)(8x+2)+5x=6x+9
We found another way to get x = 61.
(2/7)(4x + 1) + 5x = 6x + 9
x=4
(2/4)(3/1)=1x-3
I think the solution above where the solution is x = -70 is actually a case where 25x = -70, which would make x = -2.8. (9/1)(3x + 8) + 4x = 6x + 2 gives us 27x + 72 + 4x = 6x + 2, which then simplifies to 31x + 72 = 6x + 2, which further simplifies to 25x = -70. Did I miss something in my calculations?
We tried this problem today and found that x did not = -70 either. I think it was a calculation error.
One of my students found several ways to make the equation true for any number, so that you could use 100 or 1,456,918 and it would still be true:
9/3(1x + 2) + 4x = 7X + 6
6/3(2x + 4) + 1x = 5x + 8
6/2(1x + 3) + 4x = 7x + 9
Another student tried to find the lowest possible and got x = -44.
7/8(1x + 4) + 5x = 3x + 9
If you define smallest to be closest to zero, then 8/2(9x + 1) + 6x = 3x + 4 is zero.
2/9(5x+1)+6x=7x+8 is the best answer. X=70. All you have to do is just try.
A student of mine used 1/9(8x+2) = 5x+6 to get a low value of -52
A term is missing: 1/9(8x+2)+4x=5x+5 to get -52.
did you lean 6 at the end? Otherwise, you used 5 twice.
1/9(8x+2)+4x=5x+5=-52
x=61
(2/7)(4x+1)+5x=6x+9
1/2(6x+4)+5x=9x+8
x=-6
4/8(3x+4)+2x+3x+9=14
I don’t know if this is right or not but here is my answer.
In this equation x=1
1/2(4x+6)+7=9+3
x=1
1/2(2x+3)+4x=3x+3.5
My equation for x=20
(9/3)(1x+8)+2=6x+4
8/2(9x+1)+6x=3x+4
(9/1)(3x+8)+4x=6x+2
3/4(5x+9)+2x=6x+2
x=19/56
8/1(4x+8)+6x=4x+8
x=1.8666 or no solution
2/1x(6x+2)+4x=2x+4
x=no solution
1/2(2+x)=(8x)
9/1(4x+8)+4=6x+2
x=-2 thats the best answer i got
1/2(2+x)=(8x)
(8/1)(2x + 7) + 3x = 7x + 2
(9/1)(3x+8)+4x=6x+2
1/3 (5x + 6) + 4x = 2x + 9 = 3/7
(4/8)(6x + 2) + 1x = 3x + 9
and x=8
The smallest solution I’ve found so far is x = -70
(9/1)(3x + 8) + 4x = 6x + 2
That equations would give you x= -2.8
The smallest I found is x= -0.3 (repeating)
(8/1)(2x + 9) + 7x = 6x + 8
(9/1)(3x+8)+4x=6x+2
The largest solution I’ve found so far is x = 8:
(4/8)(6x + 2) + 1x = 3x + 9
The smallest equation I found was 1/9(3x+8) +4x =6x +2 which Equals -70
The largest solution I found was (4/8)(6x + 2) + 1x = 3x + 9, which equals to 8.
I mean X equals 8
1/9(8x + 2) + 4x = 5x + 7….x = -61!
My kids have found x = 70 and x = -70
1/9(3x+5)+2x=4x+5
-8/3
(9/1)(3x + 8) + 4x = 6x + 2. X= -70.