Open Middle®
Directions: Using the integers -5 to 5, at most one time each, write an expression that will have the greatest (or least) absolute value.
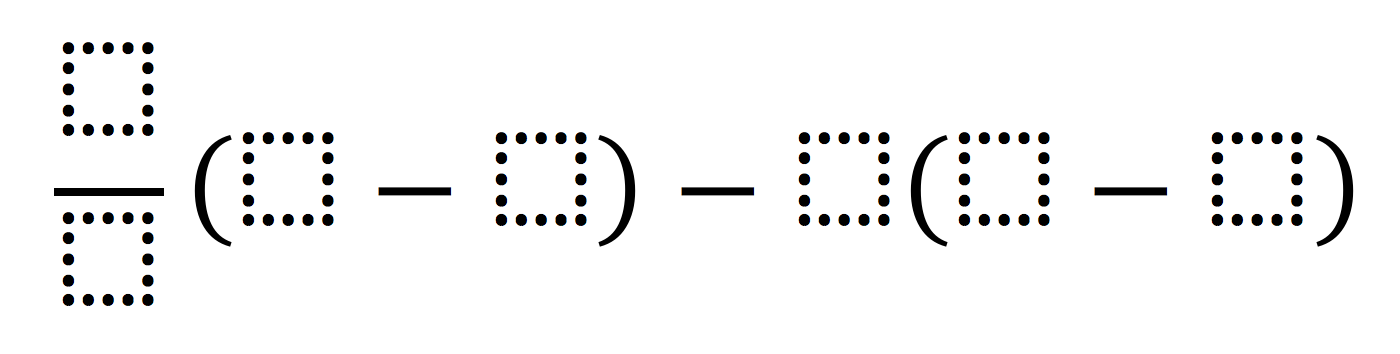
Hint
What kind of fraction produces larger (or smaller) numbers when multiplied by an integer other than 0? Which empty square in the expression has the greatest effect on the total? What does absolute value mean?
Answer
Greatest absolute value: |70| = |-70| = 70
Least absolute value: -4/2[-1 – (-2)] – 1[-5 – (-3)] = 0 (found by Jadine Louie)
Least absolute value: -4/2[-1 – (-2)] – 1[-5 – (-3)] = 0 (found by Jadine Louie)
Source: Michael Wiernicki
Is the least absolute value here zero?
-4/2[-1 – (-2)] – 1[-5 – (-3)]
Yes, your equation does have an absolute value of 0. Unfortunately though, it breaks the rule of using each number at most one time. Without that restriction, yours would definitely have a winner.
How does it break the rule? The numbers I’m seeing are -4, 2, -1, -2, 1, -5, and -3. Nothing was repeated or am I missing something?
I believe because you used the digit 2, twice. It doesn’t matter that it is a -2 and a 2 (digit is the same.
I’m with Crystal. I don’t see which number was used twice either. There are 7 slots and only 6 ‘digits’ 0, 1, 2, 3, 4, 5 if you are not assuming -1 and 1 are different numbers. So exactly which number was used twice?
All of you were right and I was wrong. I don’t know what I was seeing. Yes, 0 is the least absolute value. I’ll correct the answer. Sorry!
`-4/2[-1 – (-2)] – 1[-5 – (-3)]` is not an equation, because it doesn’t have an equals sign (this `=`) in it.
Can you give me a problem with the answer of 5 and negative 5
One of my students is wondering about this:
5/.01(4 – (-5)) – -3(2 – (-4)= 4518 whose absolute value would be 4518.
So, because the word “numbers” is used in the directions instead of digits, my student believes this solution is valid. Thoughts?
That’s not the intent of the problem but I can see her point. I’ll change it to digits.
I have an idea. You could have an absolute value of 0 if you did: -1/5(2 – -2) – 0(3 – -3)
Although this may be wrong, seen as I also agree with Jadine’s equation. I see no repeated numbers in mine or Jadine’s though.
My students came up with the following for the largest absolute value:
2/1(-5 – 0) – 3(5 – -4)= -37
Therefore the absolute value is 37.
Thoughts?
It’s so neat that this problem has generated such a great discussion! Finding a solution showing the least absolute value to be zero is amazing. Well done, everyone! And thank you for making this problem better!
@Andrea When going for the largest absolute value, I found at least three ways to make it greater than 37. I would encourage them to keep trying to see who can get a larger absolute value.
Does anyone know the answer to get 70?
I got 69.