Open Middle®
Directions: Using the digits 1 to 6, at most one time each, fill in the boxes so that top two equations are equal and the bottom equation has a greatest value than the other two.
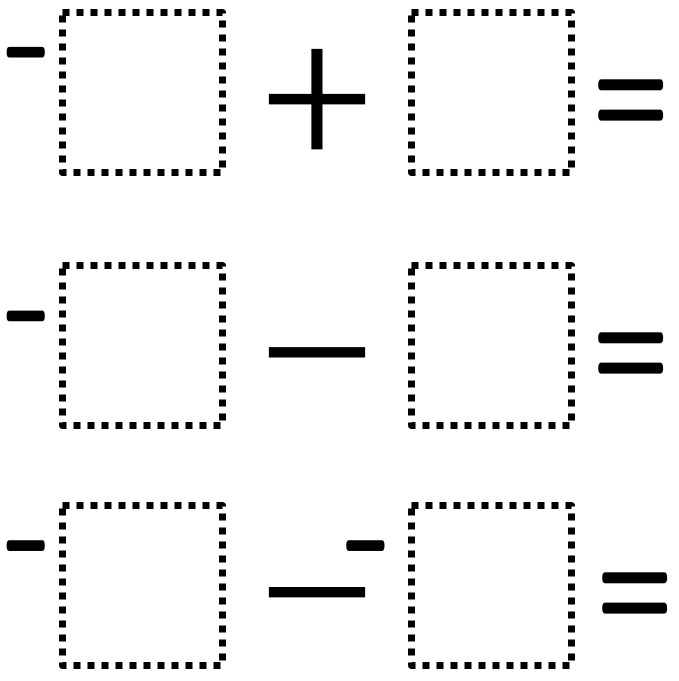
Hint
If you want the first two answers to be the same, should they both be positive or negative?
What pairs of numbers from 1-6 can you combine to make the same outcome?
How could we rewrite the second problem?
How could we rewrite the third problem?
What pairs of numbers from 1-6 can you combine to make the same outcome?
How could we rewrite the second problem?
How could we rewrite the third problem?
Answer
First possible solution:
-6 + 3 = -3
-2 – 1 = -3 (2 and 1 in any order)
-4 – -5= 1 (or -5 – -4 = -1)
-6 + 3 = -3
-2 – 1 = -3 (2 and 1 in any order)
-4 – -5= 1 (or -5 – -4 = -1)
Second possible solution:
-6 + 1 = -5
-2 – 3 = -5 (2 and 3 in any order)
-4 – -5 = 1 (or -5 – -4 = -1)
Third possible solution:
-6 + 2 = -4
-1 – 3 = -4 (1 and 3 in any order)
-4 – -5 = 1 (or -5 – -4 = -1)
Source: Kate Nerdypoo
Another one:
-6+2=-1-3=-4
and -4<-4-(-5)
Great spot Dominique – I have added your suggestion to the list of solutions.
I agree good job!
-6 + 5 = -1
-4 – (make it addition) 3 = -1
-2 – (make it addition) -1 (make positive) = -1
would also work
I agree
-1 wouldn’t be the greatest possible value, would it?
i’m not sure about the wording “greatest value,” it threw me off, thinking -1- (-6)=5 was the greatest value possible, but the other digits cannot then be used to create equivalent expressions
Good questions, however I feel as though it would be better to refer to the three EXPRESSIONS, rather than equations.
So the directions would read like this “Using the digits 1 to 6, at most one time each, fill in the boxes so that top two expressions are equal and the bottom expression has the greatest value.
I’m not sure equations should be equal or greater than other equations, it is the expressions on either side of the equations which we compare.
Agree! I also removed the equal signs when using this problem with my students.
1. -6+2=-4
2. -1-3=-4
3. -4= -4- -5
-6+3=-3,-6+1=-5, and -6+2=-4
-6+3=-3
-1-2=-3
-1.5–1.6=0.1/-5+4=-1
-6 + 3 = -3
-2 – 1 = -3 (2 and 1 in any order)
-4 – -5= 1 (or -5 – -4 = -1)
-6 + 1 = -5
-2 – 3 = -5 (2 and 3 in any order)
-4 – -5 = 1 (or -5 – -4 = -1)
-6 + 2 = -4
-1 – 3 = -4 (1 and 3 in any order)
-4 – -5 = 1 (or -5 – -4 = -1)
-6+3=-3
-2-1=-3
-4-(-5)=1
-1+6=5
-2-5=-7
-3–4=-1
1 + 2 = 3
-1 + 4 = 3
5 – (-1) = 6
🙂
1 + 2 = 3
-3 + 4 = 1
-5 + -6 = -11
AH!!!
1 + 2 = 3
6 + -3 = 3
5 + 4 = 9
-1 + 6 = 5
-2 – 5 = -7
-3 – (-4) = -1
Please…