Directions: Using the digits 0 to 9, at most one time each, fill in the boxes to make a true statement with the greatest possible total.
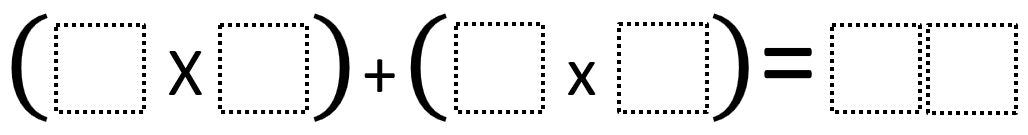
Hint
HINT GOES HERE
Answer
The greatest total we’ve found so far is 83 which comes from (9 x 7) + (5 x 4). Do you have a greater total? Let us know in the comments.
Source: Owen Kaplinsky and Robert Kaplinsky
 Open Middle®
Open Middle®



Traut Core Knowledge 4th Grade Ms. Petros’ class got 96. (9 x 8) + (4 x 6).
That doesn’t work. You used the number 9 twice
I got 115 with ( 9 x 8 ) + ( 7 x 6 )
You can’t have a 3 digit product.
An exhaustive search yields the greatest answer is (9 x 7) + (5 x 4) = 83.
Here is the code:
import itertools
max_answer = 0
valid_answer_count = 0
for trial in itertools.permutations(range(0,10),4):
answer = trial[0]*trial[1]+trial[2]*trial[3]
answer_ones = answer % 10
answer_tens = answer // 10
if (answer_ones in trial): continue
if (answer_tens in trial): continue
if (answer_ones == answer_tens): continue
if (answer > 99): continue
#print(trial,answer)
valid_answer_count += 1
if (answer > max_answer):
max_answer = answer
max_trials = trial
print(“#Valid answers:”, valid_answer_count,”Max answer:”,max_answer,max_trials)
and the result:
#Valid answers: 1144 Max answer: 83 (4, 5, 7, 9)
And here are all the unique answers with a representative expression that results in the answer:
12 = (9*0) + (4*3)
14 = (9*0) + (7*2)
16 = (9*0) + (8*2)
18 = (9*2) + (7*0)
20 = (8*1) + (4*3)
21 = (9*0) + (7*3)
24 = (9*1) + (5*3)
25 = (7*3) + (4*1)
26 = (7*3) + (5*1)
27 = (9*3) + (8*0)
28 = (9*0) + (7*4)
29 = (8*3) + (5*1)
30 = (7*4) + (2*1)
32 = (9*0) + (8*4)
36 = (9*4) + (8*0)
37 = (8*4) + (5*1)
38 = (9*4) + (2*1)
39 = (8*4) + (7*1)
41 = (9*3) + (7*2)
42 = (9*0) + (7*6)
43 = (8*1) + (7*5)
45 = (7*6) + (3*1)
46 = (8*5) + (3*2)
47 = (9*5) + (2*1)
48 = (9*5) + (3*1)
50 = (9*4) + (7*2)
51 = (9*3) + (6*4)
52 = (8*6) + (4*1)
54 = (9*6) + (8*0)
56 = (9*0) + (8*7)
57 = (9*6) + (3*1)
58 = (9*6) + (4*1)
59 = (8*7) + (3*1)
60 = (9*4) + (8*3)
61 = (9*5) + (8*2)
62 = (9*3) + (7*5)
63 = (9*7) + (8*0)
65 = (9*7) + (2*1)
67 = (9*3) + (8*5)
68 = (9*7) + (5*1)
70 = (9*6) + (8*2)
72 = (9*8) + (6*0)
74 = (9*8) + (2*1)
75 = (9*8) + (3*1)
76 = (9*8) + (4*1)
81 = (9*7) + (6*3)
82 = (9*6) + (7*4)
83 = (9*7) + (5*4)
This looks great! I’m assuming you used Python.
My 4th grade students offer this solution:
(9 X 8) + (6 X 4) = 72 + 24 = 96
Good try, but you used the 9 and the 6 both as factors and as digits in the product. You can’t repeat any of the digits used in the factors as digits of the product.
96 8 times 9 and 6 times 1
i meamt 6 times 4 and 8times 9
9 times 7 and 6 times 3 equal 81
(7×3)+(8×1)
(9×8)+(4×5)
(9×8 ) + (5×3) = 87 is what my 4th grader son was able to do.
guess got 8 twice