Open Middle®
Directions: Using the digits 1 to 9, at most one time each, place a digit in each box to make two compound inequalities that are equivalent to 2 ≤ x < 4.
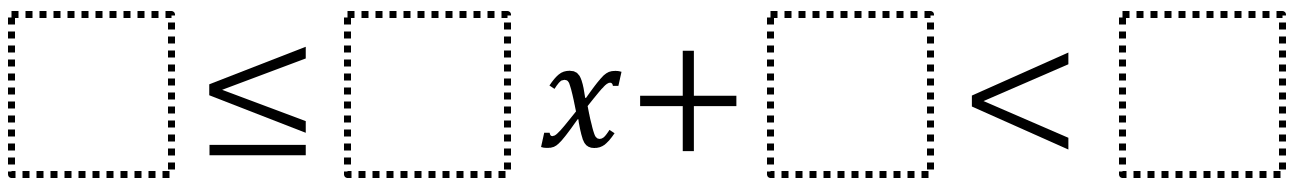
Hint
How does changing the coefficient affect the resulting value?
How does changing the constant next to x affect the resulting value?
How does changing the constant next to x affect the resulting value?
Answer
There are many answers including:
4 ≤ 1x + 2< 6 and 5 ≤ 2x + 1< 9.
Source: Robert Kaplinsky
6 <_ 2x + 1 < 9
I read this differently, I guess. I thought that I had to write an answer consisting of both inequalities without repeating any digits at all. I will have to make it clear that it is only necessary to not repeat within each inequality.