Directions: Write a quadratic equation that has a y-intercept of 24 and the distance between the x-intercepts is 10. Bonus: find more than 2 quadratic equations.
Hint
Which form of a quadratic equation is more useful in this problem?
What does the intercept mean?
What does the intercept mean?
Source: Daniel Luevanos
 Open Middle®
Open Middle®
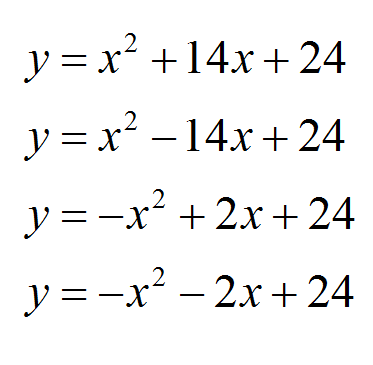



x^2-14x+24
y = (x-12)(x-2)
Y=0.96x^2 + 24
I’m writing out my thinking on the way to my 3 answers, all downward-facing parabolas (I hadn’t enough thought that it could be upward-facing!!!)
Parabola #1: So if (0, 24) is the vertex, then -5 and 5 must be the x-intercepts, so (x-5)(x+5) is part of the answer. But that’s x^2 – 25. So -(x-5)(x+5) gives -x^2 + 25. But then it needs to go through (0,24) instead of (0,25), so “a” must be 24/25. So: (-24/25)(x+5)(x-5)!
Parabolas #2 and #3: -x^2+25 can just be shifted one right or one left. So,
#2: -(x-1)^2 + 25 and
#3: -(x+1)^2 + 25 should work, but let me check.
Yes, they both have a vertex at (1, 25) and (-1, 25) respectively, and since they’re downward facing parabolas with rigid transformations that don’t stretch or compress them, you go down one from the vertex and over one in each direction in order to get the next two points, so they both have a y-intercept of 24!
But do they both have x-intercepts that are 10 apart? They should since they’re just -x^2+25 shifted one right or one left. But… for #2, 6 and -4 are the x-intercepts (they both give 5^2 or (-5)^2 which is 25, negated is -25, plus 25 is zero for y.
And for #3, it’s -6 and 4, which are 10 apart.
Ok, I’ve reasoned through and am very confident of my 3 answers. But could I get a 4th?….. I would try to think about the point 2 over and 4 down from the vertex, and getting that to line up with (0, 24), and then applying some value of a so that the x-intercepts were 10 apart. But eh, I’m tired!