Open Middle®
Directions: Fill in the boxes below using the digits 1 to 6, at most one time each, to make the largest value for D (the derivative).
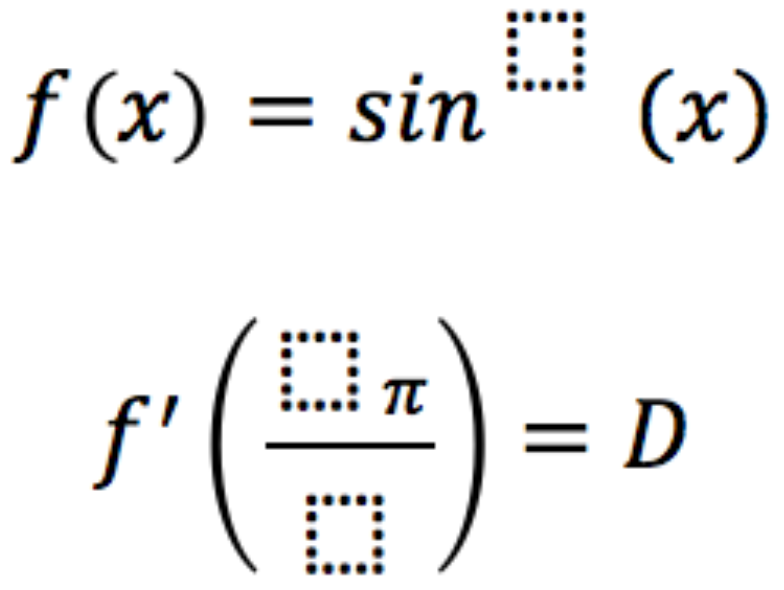
Hint
What values give an output of 1 or 1/2 to the derivative of sin(x)?
Answer
sin^6(x) and f'(4pi/2)…or sin^6(x) and f'(2pi/1)
Source: Chris Luzniak
I don’t think your answer is correct.
The derivative of f(x)=sin^6(x) is f'(x)=6sin^5(x)*cos(x)
So f'(2pi)=0 b/c sin(2pi)=0
I believe the correct answer should be f(x)=sin^6(x) and f'(1pi/3)=1.461
I agree, maximizing cosine will zero the sine function. Mr. H has the correct answer, to the best of my ability to judge.
Thanks Chris and Mr. H
I believe that f'(4pi/3) = f'(pi/3) so this provides another possible solution.
Yes, I believe that you are correct Mr. H.