Directions: Using the digits 1-9, at most one time each, fill in the blanks to make a true multiplication equation.
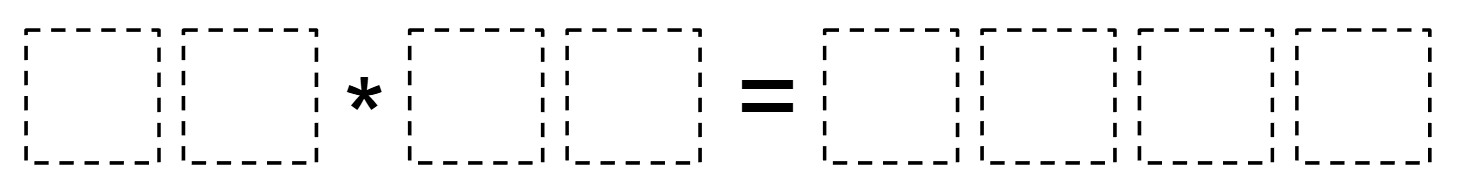
Hint
What would not work as a digit in the tens place?
Answer
Number of Unique Solutions: 12
1: 23 * 69 = 1587
2: 32 * 49 = 1568
3: 34 * 52 = 1768
4: 34 * 58 = 1972
5: 38 * 52 = 1976
6: 42 * 38 = 1596
7: 53 * 92 = 4876
8: 56 * 39 = 2184
9: 57 * 24 = 1368
10: 58 * 37 = 2146
11: 58 * 64 = 3712
12: 62 * 87 = 5394
Source: Adina R
 Open Middle®
Open Middle®



23*74 would be correct only if you didn’t have to put in the answer to the equation
23*74 is what I think the answer is
what is the math trick or strategy behind this problem and solution? how do you get to a correct answer, aside from trial and error??
Ummm the given answer, 23* 74 is not correct.
90X99=8910
90 * 74 = 6660
Good question! How DOES one deduce the correct answer without plugin & chugging their way through a list of numbers as long as the day?
I feel like you have to start with some guesses, but the thinking occurs once you begin and as you are going along. You wouldn’t just guess the two numbers to multiply, but you would at least have to start out guessing the digits in the ones places, which would lead to some thinking and reasoning as you go along.
For example, when I was working with a group of students, they chose to start with a 5 and a 9 in the ones place. They quickly discovered that it wouldn’t work since they had to have a zero in the ones place in the second partial product, which would lead to an additional 5 in the ones place in the solution. One student decided that he wanted to change the 9, rather than the 5. That led into a discussion that anything multiplied by 5 would have a product ending in a 5 or a 0. This would also not work as we already knew that we couldn’t have a 5 again in the product and we couldn’t have a 0 in the ones place of the first partial product, as that would lead to a 0 in the ones place of the final solution and 0 is not one of the digits that can used in the blanks. This in turn let him see that it was indeed the 5 that had to be changed.
I think 42 *38=1596
53 times 92 equals 4876