Open Middle®
Directions: Using the digits 0 to 9 at most one time each, fill in the boxes to make the greatest possible product.
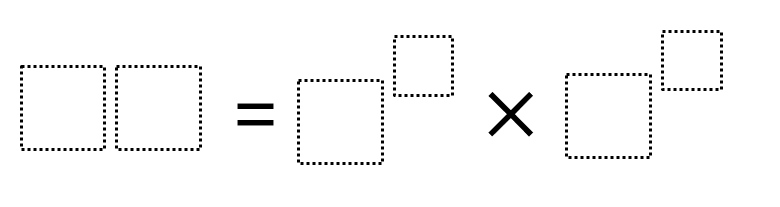
Hint
What digits would make good/bad exponents?
What digits would make good/bad bases?
What digits would make good/bad bases?
Answer
The greatest product that’s been found so far is 80 = 5^1 * 2^4.
Source: Robert Kaplinsky
Why not 96 = 2^5 x 3^1
I agree…we found that one this week, too!!! 🙂
El dijito seria el mismo porque seria 97=2 5 x 3 1
I agree
we got 81= 9^2 x 7^0
81 multiply by zero is zero
But anything (except 0)to the power of 0 is 1, not 0.
80=5^1*2^4
i did _____________=9^8×7^6
80=5^1×2^4
I 96 because 6^1 × 4^2 is equal to that.
You can only use each digit once. You used the 6 twice.
i did 96=2^5+3^1
this is very hard
Why not 96=2^5+3^1
80= 5^1*2^4
That´s exactly what i thought 96=2^5+3^1
I think it would be 80 = 5^1*2^4
5.0644e12 =
5.0644e12 =
96=2^5 x 3^1
80=5^1 * 2^4
Why is this so hard
You did a terrific job! This post seem extremely great.
I am not very sure but i am guessing that it would be 93= 2^5* 3^2 This is kinda confusing to me so i think i might be a bit off
that gives 32 * 9 = 288 which is not a 2 digit number and uses 8 and 2 twice
I did 9^2*3*2=
I got 96 = 6^1 x 4^2
You used the digit 6 twice.
I did 64=1^0*8^2 because anything to the power of one equals zero.
59= 1^0 × 8^2
50 = 2^1 * 5^2
96 = 2^5 * 3^1
Your first one doesn’t work, because you can only use each digit once, and you used 2 twice.
up i did 8⁹*6⁷ and got 37,572,373,905,408 i think i did something wrong oops
I love that one box represents only one digit. This is also a great exercise in order of operations. Thank you! It was also great that I realized the larger digits had to be the product AND the product had to be less than 100.
4^2 x 5^1 = 16 x 5 = 80
but even larger
2^5 x 3^1 = 32 x 3 = 96
I got 96=2^5*3^1 which is 32×3
2^5*3^1 = 96
we did addition in sted of multiplication so I got 4^3+2^5
I don’t think anyone has 40 = 2^3 x 5^1 which uses all of the numbers from 0-5!
Here are all the possibilities that make a true statement (except for switching the factors):
48 = 2^3 * 6^1
49 = 1^3 * 7^2
49 = 1^5 * 7^2
49 = 1^6 * 7^2
49 = 1^8 * 7^2
54 = 3^2 * 6^1
56 = 2^3 * 7^1
64 = 1^3 * 8^2
64 = 1^5 * 8^2
64 = 1^7 * 8^2
64 = 1^9 * 8^2
64 = 2^3 * 8^1
96 = 2^5 * 3^1
As you can see, 96 is the greatest.
8 is not a prime number
Jill you are correct. Any base number that is NOT prime would not be correct.
Jess Friar from Australia
96 = 2^5 \times 3^1