Open Middle®
Directions: Using the digits 0-9, no more than once, complete the puzzle so that the sum of each side is equivalent.
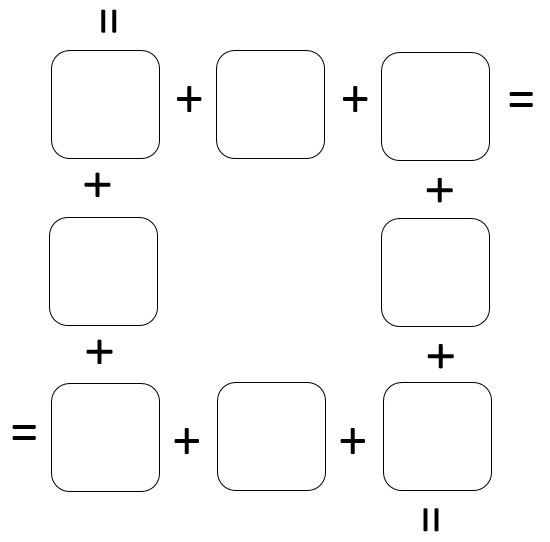
Hint
The sum of the middle numbers on opposite sides are always the same
Answer
There are multiple answers, for example, you can arrange the numbers, 0, 1, 2, 3, 4, 5, 6, 7 in such a way that the sum of each side equals 9. Another solution includes using 0,5,7,3,2,6,4,8 and have sums of 12.
Source: Joshua Nelson and Renee Owen
0,7,3,2,6,5,1,4 and each side equals 9
If each sides equals 9 then it is 0,4,5,3,1,6,2,7
0+4+5=9
5+3+1=9
1+6+2=9
2+7+0=9
I don’t understand yours. 0,7,3,2,6,5,1,4. Can you explain please?
0+7+3=10
3+2+6=11
6+5+1=12
1+4+0=5
0+7+2=9
6+3=9
5+4=9
0,7,4,6,1,2,8,3 and each side equals 11.
0+7+4=11
8+1+2=11
6+3+2=11
5,4,6,9,0,8,7,3
15
0+8+7=15
9+6=15
5+4+6=15
4+8+3=15
9 2 1
3 6
0 7 5
9+2+1=12
6+5+1=12
0+7+5=12
9+3=12
5, 3, 9 – 9, 1, 7 – 7, 2, 8 – 8, 4, 5 with each side = 17
Has anyone really used this with 1st graders? If so, with an entire class or just a select few?
I’m trying it tomorrow with second graders. We’ve done Ken Ken and I think this will be even more challenging because it is so open ended…
9+8=17
5+3+9=17
9+1+7=17
7+2+8=17
0 ,5,4,3,2,6,1,8,0
I think it is 9
9+8=17
5+3+9=17
9+1+7=17
7+2+8=17
5+4=9
3+6=9
0+1+8=9
0+8+3-2=9
2 5 3 6 1 9 0 8 2 = 10
1+9=10
9+2-1=10
6+8-5+1=10
0+3+6+1=10
90354621 equals 12
9+0+3=12
5+4+2+1=12
6+5+3-2=12
3+5+4=12
I did each side equals 17
7+4+6
1 3
9+0+8
Sums = to 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 are all possible
1+3+6+8=17
7+9+1=17