Directions: Using the digits 1-9, at most one time each, complete the first three terms of the arithmetic and geometric sequences. What sequences result in the greatest sum of their second terms? (e.g. 3, 5, 7 and 2, 6, 18 would result in a sum of 5 + 6 = 11). What sequences result in the least sum of their second terms?
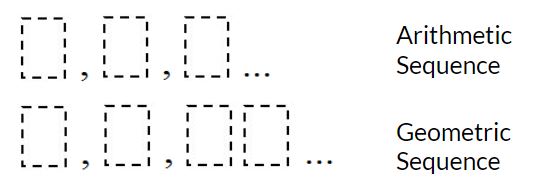
Hint
The maximum sum would be 17, with the 8 and the 9 digits as the second terms of each sequence. Can this be done? There are only six possible geometric sequences with the given constraint… what are they?
Answer
The greatest sum is 15. There are three ways to get this: 4, 6, 8 and 3, 9, 27; 5, 7, 9 and 4, 8, 16; and 5, 7, 9 and 1, 8, 64. The least sum is 10. There is one way to get this sum: 3, 4, 5 and 2, 6, 18.
Source: Erick Lee
 Open Middle®
Open Middle®



It seems as though the solution to the least sum is incorrect, as the number 1 is used twice.
I found the patterns 0,3,6 and 1,2,4 with a least sum of 5.
Here is it true that the geometric sequence would need to be a double digit number?
We also agree that the least sum is incorrect, as it violates the rules and uses the 1 twice. We are also debating whether “08” is a two digit number, thus using 1, 3, 5 and 2, 4, 08, and having a sum of 7. Still working! 🙂
My students found the following produces the least sum:
3,5,7
1,2,04
I’ve changed the instructions to remove the question of whether a two-digit number can begin with 0. I’ve also fixed the answer. The least sum is now 10.
My students today were finding examples that had negative common differences, i.e. 9,7,5 and 4,8,16. Expands the correct answers quite a bit!
0 is not a number 1-9