Directions: Using the digits 0 to 9, at most one time, fill in the blanks to create sine and cosine functions with the given periods in degrees.
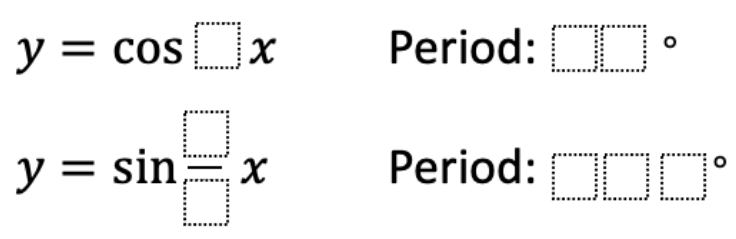
Hint
Which function has more possible answers? Therefore, where is the smartest place to start?
Many numbers for b will result in a period with last digit 0, but you can only use 0 one time, so you can not have two periods that have the last digit 0. What insight might this give you about what numbers to start with?
Answer
Option 1 for cosine function y=cos 4x yields two possible solutions:
y=cos 4x with a period of 90° & y=sin 5/3x with a period of 216°
y=cos 4x with a period of 90° & y=sin 8/7x with a period of 315°
The related option for the cosine function y=cos 9x gives us:
y=cos 9x with a period of 40° & y=sin 5/3x with a period of 216°
y=cos 9x with a period of 40° & y=sin 8/7x with a period of 315°
For the cosine function y=cos 5x, we have the following solutions:
y=cos 5x with a period of 72° & y=sin 6/3x with a period of 180°
y=cos 5x with a period of 72° & y=sin 9/4x with a period of 160°
y=cos 5x with a period of 72° & y=sin 3/8x with a period of 960°
y=cos 5x with a period of 72° & y=sin 4/9x with a period of 810°
Finally, for the cosine function y=cos 8x, we can find:
y=cos 8x with a period of 45° & y=sin 3/6x with a period of 720°
y=cos 8x with a period of 45° & y=sin 9/3x with a period of 120°
Source: Kate Nerdypoo
 Open Middle®
Open Middle®


