Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make the smallest (or largest) quotient.
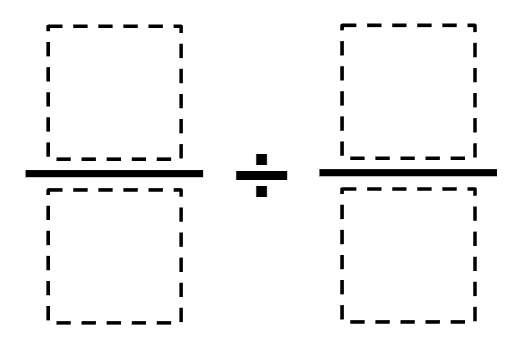
Hint
How can we tell whether it would be better to put the larger/smaller numbers in the numerator or denominator?
Answer
Smallest: 1/9 ÷ 8/2 or largest: 8/2 ÷ 1/9 (Thank you to Kim Abrams for pointing out a mistake in the answer.) Julie Wright also points out that there are multiple correct answers stating that “it seems like putting the 1 & 2 in the numerator of the first fraction and the denominator of the second in either order, and putting the 8 & 9 in the other spots in either order, will always give (1*2)/(8*9) or 1/36.”
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Mr. Kaplinsky, please check to see if you mistyped your answer to this problem. We think the answer is 1/9 divided by 8/2. (I certainly could have made an error as well). Thanks for checking this!
You are totally right Kim. Thank you so much for pointing this out. I have updated the answer and gave you credit.
Aren’t there multiple correct answers? It seems like putting the 1 & 2 in the numerator of the first fraction and the denominator of the second in either order, and putting the 8 & 9 in the other spots in either order, will always give (1*2)/(8*9) or 1/36.
That is a great realization Julie! The lesson I am learning is that it is much easier to create some of these problems than it is to find all the answers! Thanks.
I’m sure we’ve all been there. I love your ideas and that you are putting it all together. My kids were incredibly engaged with the mixed number sum problem yesterday, especially the ones who really needed a challenge. I let the ones who came up with the highest sum skip some homework problems!
Some of my students tackled this problem, and one found 4 solutions that all get 36, the largest quotient:
9/2 divided by 1/8
8/2 divided by 1/9
8/1 divided by 2/9
9/1 divided by 2/8
All her math looks great, please double check to make sure I didn’t miss something. Thanks for providing resources like these!!
That seems fine to me Matthew. Thanks for sharing!