Open Middle®
Directions: Place an integer in the blank to find the largest and smallest value that will make the quadratic expression factorable.
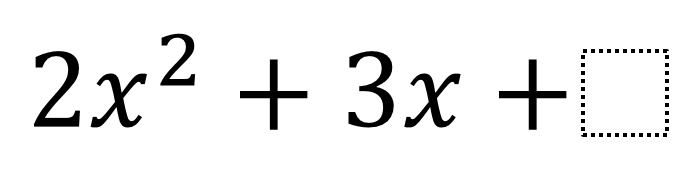
Hint
How would you represent this problem using visually (such as by using algebra tiles)?
What patterns are you observing for the maximum and minimum values of C?
What patterns are you observing for the maximum and minimum values of C?
Answer
The largest C can be is 1. You can continue to find smaller and smaller values of C, so the smallest value of C is negative infinity.
Source: Robert Kaplinsky
if you are OK with fractions..i.e. factoring does not require integers the value of c = 1 1/8 also works.
Also if you factor with complex numbers there are infinite values of c > 1.
c = 2 yields solutions of x = {-3+/- Sqrt (-7) } 4 , which in turn can be factors…ugly ones, but factors none the less.
The directions say integers