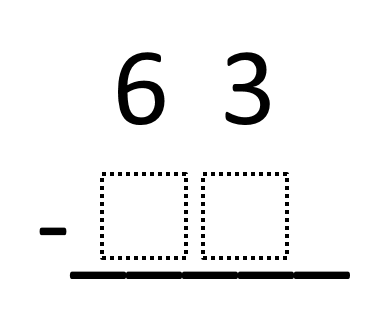
Directions: Fill in the boxes so that you would need to regroup when you subtract. Make sure that your number is less than 63.
Extension: Explain why you need to regroup using your number.
Hint
What number can you NOT subtract from 3?
Answer
The student puts in a number less than 63 and does not contain a 0, 1, 2, or 3 in the ones place.
Source: Chase Orton
 Open Middle®
Open Middle®



Awesome problem. However, the hint just perpetuates the misconception that you can’t subtract a bigger number from a smaller number. I see this misconception follow some students even through middle school. It’s ok to tell students that later they will be subtracting 7 from 3 and getting -4. This is not a foreign concept to students. Think of temperature or games where you lose points and can drop below 0.
That’s a great point Michael, and a really bad oversight on my part. I’m a big proponent of not teaching students rules that expire (ie, to multiply by 10, just add a zero) and rules limit conceptual understanding and fluency.
What might be a better hint we could put in there instead?
Chase I had the adding zero thing, but I want to teach this in a better way! If you have any ideas for me, hit me up on twitter! @nancy_estepa!
When you have the updated hint, we’ll make the change. Certainly challenging to get the wording just right.
Maybe the hint should not be worded as subtracting a number, but rather subtracting a digit. For example: What digit cannot be subtracted from 3 without regrouping? A larger digit in the ones place requires a student to regroup since this is a 2-digit by 2-digit subtraction problem. What do you all think?
How about:
HINT: Have the student represent 63 in a drawing or build it with manipulatives. “Think of a number that you could subtract from 63 without regrouping.” Offer an example if necessary. Then: “Think of a number that would would require regrouping.”
Thoughts? And you’re right. The language can get tricky.
63 – 24 = 39