Directions: Using the digits 1 to 9, at most one time each, fill in the boxes to find the largest (or smallest) possible values for the sum of x and y.
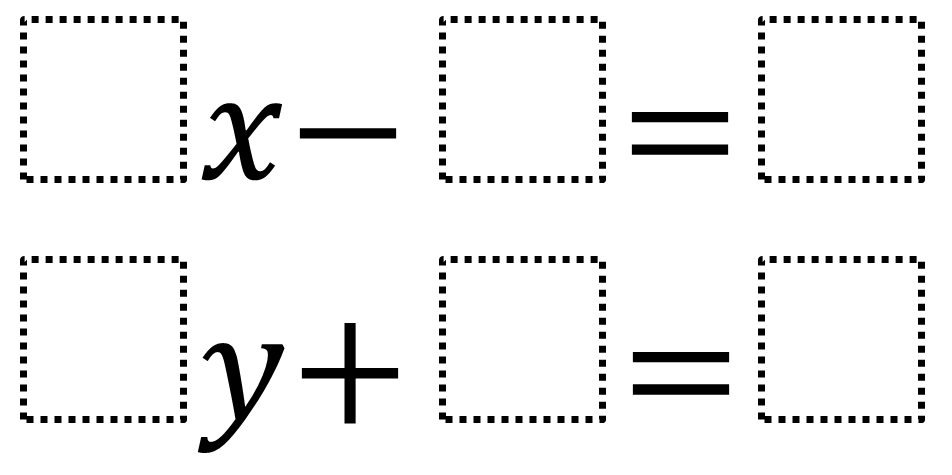
Hint
Where do you want to put the largest numbers? Where should you put the 1 and the 2?
Answer
The largest value is 19 which can be achieved by the following:
1x-8=9 and 2y+3=7
1x-8=9 and 2y+3=7
The smallest value is -6.125 which can be achieved by the following:
8x-3=4 and 1y+9=2
Source: Erick Lee
 Open Middle®
Open Middle®



Just a note that the second equation with the y value should have a subtraction sign vice an addition sign in order for the solution to be correct. (__y – __ = __)
Sorry, I mean the first equation with the x. oops.
Thanks for the heads up. I just fixed it.
I believe the answer should be as follows (this combines the results from TWO-STEP EQUATIONS 1 and TWO-STEP EQUATIONS 2):
The largest possible sum is 24, achieved with the following equations:
1x – 9 = 8 or 1x – 8 = 0 –> x = 17
1y – 2 = 9 –> y = 7
The least possible sum is -6 2/3, achieved with the following equations:
9x – 1 = 2 or 9x – 2 =1 –> x = 1/3
1y + 9 =2 –> y = -7
Woops! I take that back. In the attempt that I cited as an answer, I ignored that I can’t repeat numbers that I’ve used already. That adds to the complexity!
My brain just grew. =)
I think finding the smallest positive value would add to this problem.
9x – 1 =2 and 8x +3 = 4 11/24 or .46
1x – 5 = 4
x = 9
2y + 2 = 8
9 + 3 = 15
I can only use numbers 1-9 once and i cant use negative numbers right( 1-9 it doesn’t say negative).
Were allowed to use negatives for this equasion right?
7x – 6 = 8
x = 2
4y + 5 = 9
y = 1