Open Middle®
Directions: Using the digits 1 to 9, at most one time each, fill in the boxes so that the values of the two functions are equivalent
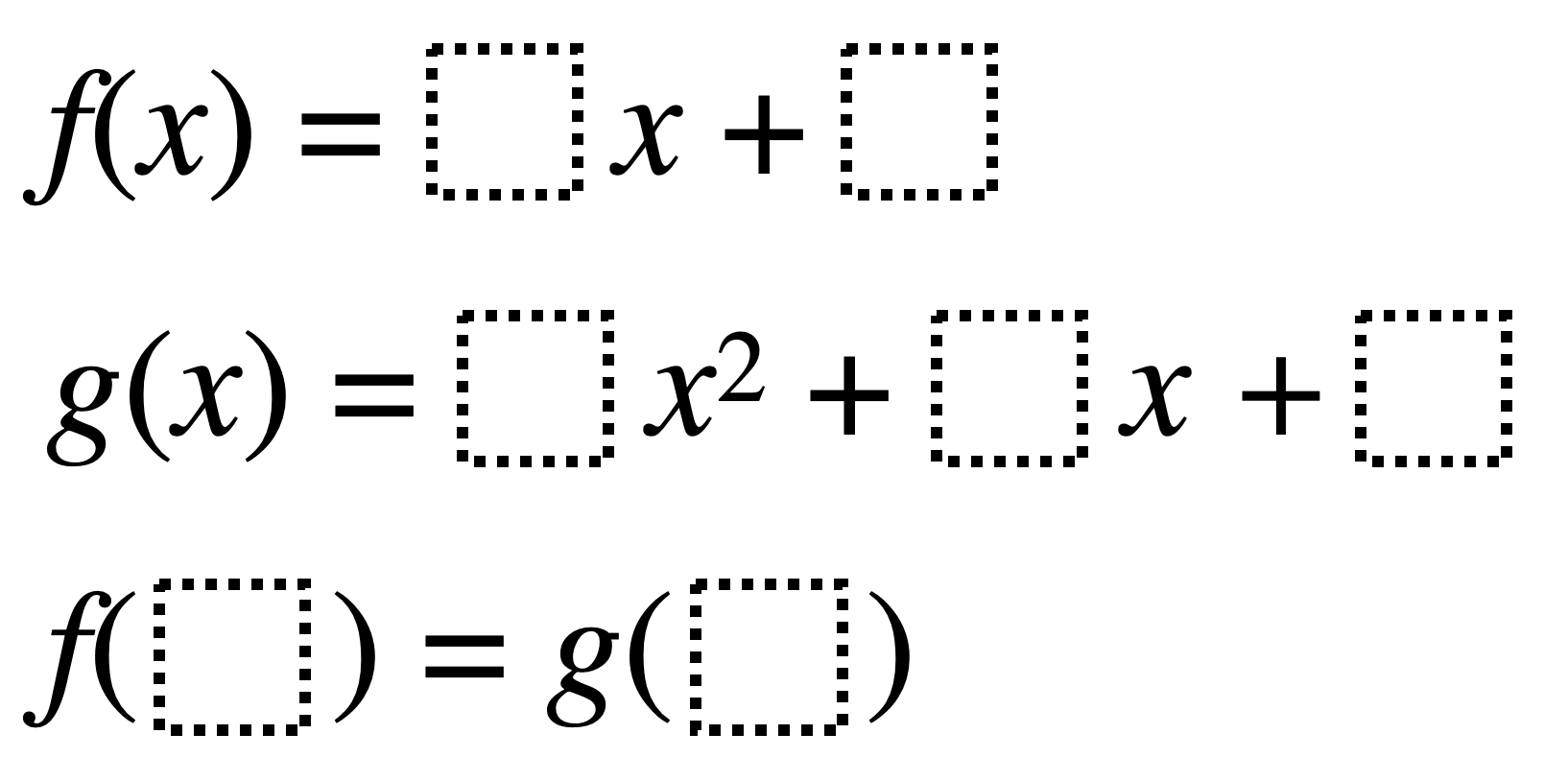
Hint
How do you use function notation to determine the input and output of a function?
Answer
One possible answer is:
f(x) = 9x + 4
g(x) = 7x^2 – 1x + 5
f(3) = g(2)
f(x) = 9x + 4
g(x) = 7x^2 – 1x + 5
f(3) = g(2)
Post any others in the comments.
Source: Steven Midzak
I think the format is confusing, and the answer uses incorrect notation and the two functions are, in fact, never “equivalent”. Rephrase like this?
Fill in spaces with whole numbers 1 – 9 only one time, so that the final equality is correct.
f(x) = ___ x + _____
g(x) = ___ x^2 – ____x + _____
f(____) = g(_____)
I agree. I like the format you used better Tim.
Thank you for this suggestion. I’ve edited the question accordingly.
It doesn’t appear to be edited.
f(3) = 2x + 4
g(1) = 7x^2 – 6x + 9
F(3)=9x+4 g(2)=7x^2-1x+5
f(9)=1x+3
g(2)=4x^2-5x+6
𝑓(3)=7𝑥+6 𝑔(2)=5𝑥^2−1𝑥+9
𝑓(8)=6𝑥+4 𝑔(5)=2𝑥^2−1𝑥+7
I gave this to my IM3 classes today, here are some they came up with that are NOT listed above:
f(3) = 6x + 1 g(4) = 2x^2 – 5x + 7
f(8) = 2x + 3 g(6) = 1x^2 – 4x + 7
f(1) = 3x + 6 g(2) = 4x^2 – 8x + 9
f(2) = 3x + 4 g(1) = 7x^2 – 5x + 8
f(2) = 3x + 7 g(5) = 1x^2 – 4x + 8
May I ask how you got your solutions
I should have looked at the solutions earlier. That negative before the x term in the quadratic makes all the difference as per Tim’s comment waaaaay back. I wonder why the question as posted still shows the +.
Thank you for this site, it is awesome!
While the negative sign does make it easier, it is possible to solve with the + in g(x) as originally listed.
f(x) = 7x + 2; g(x)=1x^2 + 3x + 4
f(6) = g(5) = 44
f(x) = 8x + 5; g(x) = 3x^2-x+9
f(6) = g(4) = 53
Love the problem and this site. Thanks.
I gave this to my 8th graders today and one of the students took off with it and ran. He wrote a program that generated 988 possible answers. And that’s why open middle questions can be so much fun. So many ways to do this yet it still stumped a lot of my students at first.
Wow! I’m curious, are all the 988 possibilities within the constraints of the problem (no repeating digits)?
There are 36 ways to pick 7 digits out of 9, and there are 7! ways to arrange each set of 7 digits, so (36)(7!)=181,440 total possible arrangements that do not repeat a number.
You can also do 7P9 to do the number of permutations when using seven of the nine possible digits. Of course, this has the same outcome of 181,440.