Directions: Using the digits 1 to 9 at most once each time, fill the boxes to make the greatest possible product.
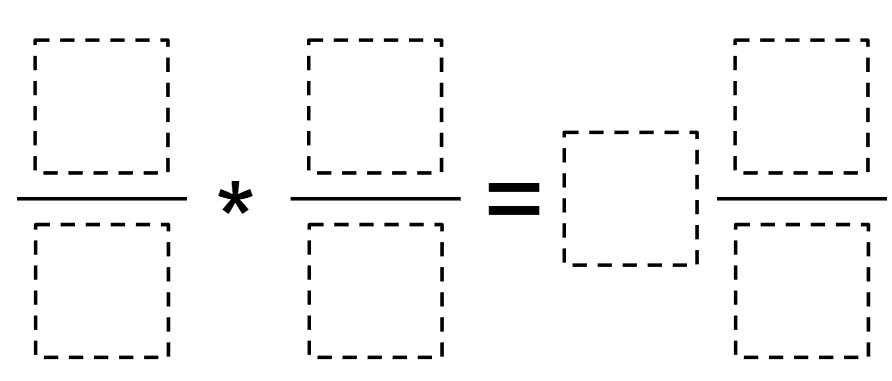
Hint
What denominators can you use that will make a one-digit denominator?
Answer
Once answer is 9/4 * 7/3 = 5 2/8.
Source: Marc DeArmond
 Open Middle®
Open Middle®



my problem was 8/5 x 6/4= 2 2/5. I know my numbers repeat and we have to find a way to not repeat a number but i got stuck and couldn’t think of another answer. My strategy was to use the answer given to help and then take one away from 9 making it an 8 and putting it over the 4 and taking one away from the 7 and putting it over the 3 and trying that. My strategy didn’t work. This was a really hard puzzle.
I had 6/2 x 3/1 = 9. I got this by finding a number that times by something would be under ten. I first got 6/2 and that got me 3. Then i got 3 from 3/1. Lastly i multiplied 3 by 3 and got 9. I agree it was a challenging puzzle.
I got 9/4×7/3=5 2/8
I got 9/4 x 7/3 = 5 2/8
I got this 9/4×7/3=5 2/8
good its great site
right
I got 9/4times 7/3=5 2/8
For my answer to that question I got 9/4 x 7/3 = 5 2/8. I got that by trying to make a very high number with the digits multiple times. At last I got one that when simplified, not all the way had no repeating digits.
I got 9/4 x 7/3 to equal 5 2/8. I got it by multiplying multiple ways over and over and once I got to 9/4 x 7/3, I realized 9×7= 63, 3×4=12, and 63/12= 5 3/12= 5 1/4= 5 2/8.
9 1/3
i did 9/1 x 8/2= 36
5 2/8
I got 9/4 x 7/3 equals 1 2/8
I got 9/4 * 7/3 = 5 2/8 because this is the highest umber you will get while using numbers 1-9 once.
9/1 x 9/1 = 81/1
I meant : 9/1 x 8/2 = 144/2 = 72
I got 5 1/4
i got 5 2/8
I got 5 1/4 which changed to 5 2/8 to not repeat a number.
didnt mean to right this one
4 1/2 x 2/3= 9/2×2/3=18/3=3
9/4 X 7/3=63/12 =5 3/12
5 2/8
I got 3 1/6 and I had the numbers 2 &7 left over
9 1/3
I did 4/3 x 5/6 which is 7 1/2
I got 9/4 x 7/3 which equals 5 2/8.
Same!
2/3 * 3/4 = 1 5/12
2/4 * 3/5 = 1 2/20
I did 7/3 *4/1=9 2/6
Nice math work!
4/1 * 7/3 = 9 2/6
I had a student give me 6/4 * 7/1= 9 3/2
I made 2\4*1\3=5\6
One of my students got 9/2 X 5/3 = 42/6= 7 and 3/6 which he replaced with 7 and 4/8 to avoid repeated digit but 3/6 is still equal to 4/8.
5/1 x 3/2 = 7 4/8
4/1 X 8/4 (or, 4 X 2) is 8 and 0/5
A student of mine did 3/1 x 5/2 = 7 4/8. Higher than anything I’ve seen!
I got 7/6 * 8/4 = 2 1/3. I don’t see that anywhere in this list, but it seems to fit the requirements.
If you don’t allow the fractional part of the mixed number to be an improper fraction, there are only these 24 solutions, ranging from 1.555… to 9.333…:
4/6 * 7/3 = 1 5/9 = 1.5556
5/4 * 8/6 = 1 2/3 = 1.6667
4/3 * 8/6 = 1 7/9 = 1.7778
3/4 * 5/2 = 1 7/8 = 1.875
5/4 * 9/6 = 1 7/8 = 1.875
6/8 * 9/3 = 2 1/4 = 2.25
7/6 * 8/4 = 2 1/3 = 2.3333
7/6 * 8/4 = 2 3/9 = 2.3333
3/6 * 5/1 = 2 4/8 = 2.5
4/8 * 5/1 = 2 3/6 = 2.5
5/6 * 9/3 = 2 4/8 = 2.5
7/6 * 9/4 = 2 5/8 = 2.625
3/9 * 8/1 = 2 4/6 = 2.6667
2/1 * 7/3 = 4 6/9 = 4.6667
6/9 * 7/1 = 4 2/3 = 4.6667
3/4 * 7/1 = 5 2/8 = 5.25
7/4 * 9/3 = 5 2/8 = 5.25
7/6 * 9/2 = 5 1/4 = 5.25
4/6 * 8/1 = 5 3/9 = 5.3333
3/2 * 5/1 = 7 4/8 = 7.5
5/2 * 9/3 = 7 4/8 = 7.5
5/6 * 9/1 = 7 2/4 = 7.5
5/6 * 9/1 = 7 4/8 = 7.5
4/3 * 7/1 = 9 2/6 = 9.3333
Of course you can get 8x as many if you swap the fractions, the numerators or the denominators of the product on the left side.
If you allow the fractional part of the mixed number to be an improper fraction, there are another 38 solutions (times 8, if you swap numerators, denominators or the entire fractions):
3/2 * 9/6 = 1 5/4 = 2.25
6/8 * 9/3 = 1 5/4 = 2.25
6/9 * 7/2 = 1 4/3 = 2.3333
4/6 * 8/2 = 1 5/3 = 2.6667
6/9 * 8/2 = 1 5/3 = 2.6667
5/6 * 8/2 = 1 7/3 = 3.3333
5/9 * 6/1 = 2 4/3 = 3.3333
4/8 * 7/1 = 2 9/6 = 3.5
6/4 * 7/3 = 1 5/2 = 3.5
7/6 * 9/3 = 1 5/2 = 3.5
5/8 * 6/1 = 2 7/4 = 3.75
6/3 * 9/4 = 1 7/2 = 4.5
4/6 * 7/1 = 2 8/3 = 4.6667
6/9 * 7/1 = 2 8/3 = 4.6667
6/8 * 7/1 = 3 9/4 = 5.25
6/8 * 9/1 = 5 7/4 = 6.75
6/3 * 7/2 = 5 8/4 = 7.0
7/4 * 8/2 = 5 6/3 = 7.0
5/4 * 6/1 = 3 9/2 = 7.5
5/6 * 9/1 = 4 7/2 = 7.5
3/1 * 6/2 = 7 8/4 = 9.0
6/2 * 9/3 = 4 5/1 = 9.0
6/2 * 9/3 = 5 4/1 = 9.0
6/2 * 9/3 = 7 8/4 = 9.0
8/4 * 9/2 = 3 6/1 = 9.0
8/4 * 9/2 = 6 3/1 = 9.0
8/4 * 9/2 = 7 6/3 = 9.0
4/2 * 5/1 = 7 9/3 = 10.0
4/2 * 5/1 = 8 6/3 = 10.0
5/3 * 6/1 = 8 4/2 = 10.0
5/4 * 8/1 = 7 6/2 = 10.0
5/4 * 8/1 = 7 9/3 = 10.0
3/1 * 7/2 = 9 6/4 = 10.5
6/4 * 7/1 = 8 5/2 = 10.5
6/4 * 7/1 = 9 3/2 = 10.5
7/6 * 9/1 = 8 5/2 = 10.5
8/3 * 9/2 = 5 7/1 = 12.0
8/3 * 9/2 = 7 5/1 = 12.0
Some of these answers are incorrect and REPEAT the digits. Does anyone have an actual answer for this problem?