Directions: Using the digits 1 to 9, at most one time each, fill in the boxes to create an equation such that the solution is as close to zero as possible.
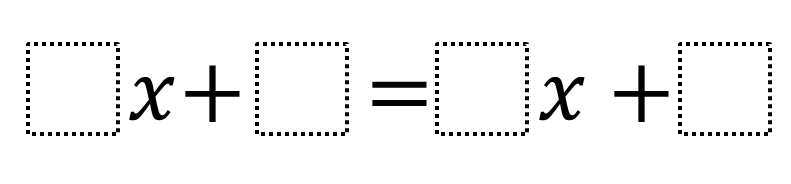
Hint
Which kinds of numbers are closer to zero?
How does the digit you choose for the constant or coefficient affect the solution’s value?
How does the digit you choose for the constant or coefficient affect the solution’s value?
Answer
There are many equations that will get to the correct answer of 1/8 or -1/8. Here are some possible equations examples:
9x + 3 = 1x + 4
1x + 7 = 9x + 8
Source: Daniel Luevanos
 Open Middle®
Open Middle®



5x+2=4x+4
I’m not sure you read the directions closely enough. First that solution is fairly far from zero. Additionally, you cannot reuse 4.
9x + 3 = x + 2
Anon is right
You are correct Anon is right.
If this is a question
5x+2=4x+4
_4. _4
X+2=4
_2. _2
X=2
I will find you
2x+4=x+8
-x -x
_________
1x+4=8
-4 -4
________
1x=4 x=4
1 1
4x+2=5x+3
9x+3=1x + 4
1x+1=3x+2
I’m new to open middle, can you combine digits and use, for example 987x and 1x?
No Scott, only one number per box.
Wouldn’t 1/9 or -1/9 be closer to 0 than 1/8 or -1/8? What about the equation 9x+2=0x+1?
nevermind just re-read that it was 1-9 not 0-9. The desmos version includes the 0.
Yeah, that one is similar but different.
1x+7= 9x+8
9x + 3 = x +2
9x + 3 = x + 2
9x+8=1x+7
7x – 4 = 3x – 6
Can we have a different equation from the problem across the equal sign ?
8x + 4 = 5 – 2x
8x+4=5-2x
1x+1=1x+1
You can only use each number once, you used 1 four times. Also, zero is not the only solution to yours.
9x+3=1x+4
1x+7=9x+8
6x+4=1x+9
1x+7= 9x+8
7x+4=5x+7
4x+6=2x+8
3x+8=9x+5
0.5
3x+1=2x+1
1x+1=3x+2
x+1=3x+2
9x+3=1x+4
2x+4=4x+5
I meant x+1= 2x+1.
I put the answer for a different question
2x+2/87816=3x+1/87816?
3x+2.00000004=4x+2
1x+2=3x+4
x+2=9x+3
6x+3=5x+2
x+4=9x+3
9x+3=x+2
1x + 7 = 9x + 8
9x+5=x+6
7x+8=5x+7
7x+1=2x+1.5
9x+5=x+4
9x+7=x+8
9x+3=1x+3
9x + 3 = x +2
8x+5=x+5
9x+1=x+6
9x+5=x+4
x+1=3x+2
7x+.5=7x+.45
9x+7=x+8
10000x + 1 = x +2
250x+29=-750x+28
9x+2=x+3
7x + 1 = 6x + 3
9x+1/4=10x+1/8
9x+4=x+5
6x+3=5x+2
7x+5=2x+4
2x +5 = 3x + 4.9
-x = -0.1
x= 0.1
9x+7=2x+8
1x+4=9x+3
2x+3=x+4
9x+2=x+1
9x+3=8x+4
wait, how is 1/8 or -1/8 the closest to zero?
5x+2= 4x+4
x+1.1/4 = 2x+1 1/2
7x+1=2x+3
1x + 7 = 9x + 8
Create an Equation with a Solution Closest to Zero
Directions: Using the digits 1 to 9 at most one time each, place a digit in each box to create an equation such that the solution is as close to zero as possible.
_ x+ _ =_ x + _ -> original problem
3x +5 = 8x +6 -> my attempt
9x+3=1x + 4
x+7=9x+8
9x+1=2x+3
9x-2x=3-1
7x=2
x=2/7
x=0,28
1x + 2 = 3x + 4
8x+1=3x+2
5x+1
x=0.2
987654x + 2 = 1x + 3
x=.0000010125…
Had the question been worded “fill in each box with one digit,” then the correct answer would have been something like
9x + 2 = 1x + 3
x = 1/8
I like the way you think. Well done. We as math teachers should be aware when the directions are not clear.
9x + 7 = 1x + 8
8x = 1
x = 1/8