Open Middle®
Directions: Use the integers -9 to 9 at most one time each, place an integer in each box to make a positive real number product and then repeat the process to make a negative real number product. You may use all the integers each time.
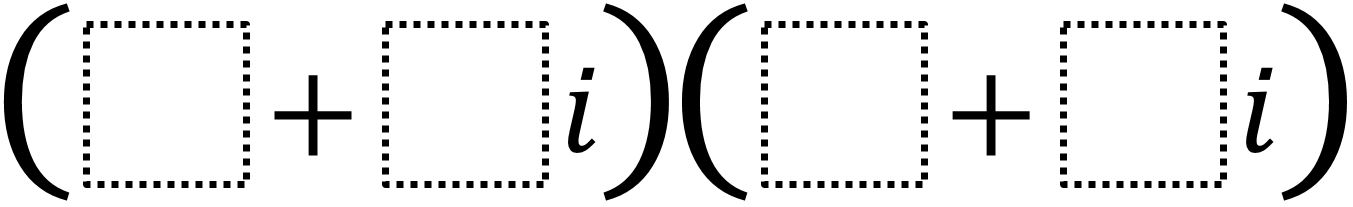
Hint
What has to happen to the imaginary terms to make a complex number a real number?
How can we accomplish that?
How can we accomplish that?
Answer
There are many answers but what has to happen with all of them is that the products of the real and imaginary terms have to eliminate each other.
An example of a negative product is (-6 + 4i)(3 + 2i). This has a product of -18 + -12i + 12i + 8i^2 which is equivalent to -18 + 8i^2 or -26.
An example of a positive product is (6 + 4i)(3 + -2i). This has a product of 18 + -12i + 12i + -8i^2 which is equivalent to 18 + -8i^2 or 26.
Source: Robert Kaplinsky
