Directions: Using the digits 1 to 9, at most one time each, fill in the boxes to create a true number sentence with the greatest possible value.
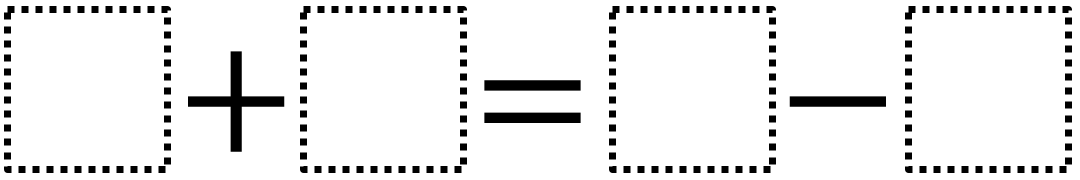
Hint
How do we know if both sides of the equal sign have the same value?
What is the greatest possible value each side of the equal sign can have?
Answer
2 + 6 = 9 – 1
6 + 2 = 9 – 1
3 + 5 = 9 – 1
5 + 3 = 9 – 1
4 + 4 = 9 – 1 is not an answer because the 4 is used twice.
There might also be conversations about whether 2 + 6 = 1 – 9 is an answer. This may lead into conversations about how addition is commutative (1 + 4 equals 4 + 1) but subtraction is not (1 – 4 does not equal 4 – 1).
What students MIGHT think is correct, but is NOT correct is something like:
4 + 5 = 9 – (any number other than 0)
This would be because 4 + 5 = 9. However, both sides of the equal sign must have the same value, and they do not when you subtract another number other than zero.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



This is a great problem. I attempted it with both first grade and second grade near the end of the school year. All year my first grade teachers have been using “is the same as” or “is the same value as” for the equal sign but my second grade teachers have not. As a result, this problem was actually much easier for grade 1 students. The group of second graders had a great deal of difficulty coming up with something other than 4 + 5 = 9 -1 for example. My first graders were able to give some examples within 30 seconds.
They are now working on finding an organized way to find all possible answers.
Thanks
5+3=9-1