Directions: What numbers go in the blanks to make the equation true?
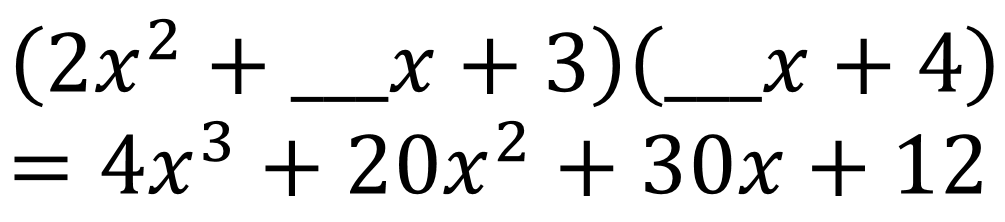
Hint
How would using a visual representation like algebra tiles or an array method make this easier to factor?
Answer
The first blank is 6 and the second blank is 2.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



This is High School? Then if they have a clue about algebra I would expect them to see this as a problem with 2 unknowns, call them A and B, multiply out the factors and solve the resulting equations. In fact by looking at the x cubed term it is “obvious” with this approach that the second number is 2. Anyway, the hint is odd as we have the factors already.
Thanks again for your contributions Howard. Clearly there are many ways to solve these problems.
I like this problem, especially if we use the area model for representing the distributive property of polynomial multiplication. We are about to start factoring this week, I may try this one!
I’d love more examples of factoring questions like this! I didn’t see any more here but if you have another place to look, let me know. 🙂
I took a stab at writing one, not sure how good it is though:
Given 12x^2 + Ax + 20 = ( x + )( x + ), and using integers -9 to 9 at most once each, create a product where A is
a) ODD
b) EVEN
c) as SMALL as possible
d) as LARGE as possible
I confess I haven’t tried it out myself but I thought it would be fun to try!
OK I think I’d have to change the last number from 20 to maybe 21, for an ODD middle term to be possible. 🙂