Directions: Using the digits 1 to 9 at most one time each, place a digit in each box to create an equation with a solution that’s as close to zero as possible.
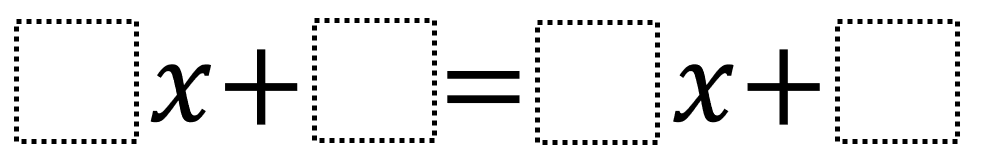
Hint
How does choosing the coefficient values affective whether the solution is positive or negative? How does choosing the constant values affective whether the solution is positive or negative?
Answer
The solution whose value is as close to zero as possible is 1/8 and -1/8. You can get that via answers like 9x + 5 = 1x + 4.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



I find myself rearranging the boxes into a different form for these problems that involve algebra. Probabl,y this is something only an expert in math would do….I don’t suppose my HS students would do this, but perhaps if they witnessed some solutions that were shown this way, they might. After finding the (or a) solution, I return it to its original form.
If rearranged, an equivalent problem is x = (▯-▯) / (▯-▯).
Therefore, we try to make x close to 0, which means the numerator should be made as small as possible, so 1 or -1 (of which there are many ways to do this, and the denominator should have a difference whose absolute value is as large as possible (so 8 or -8).