Open Middle®
Directions: Using digits 1-9, at most one time each, place a digit in each box to create two functions that do not intersect and have the following values.
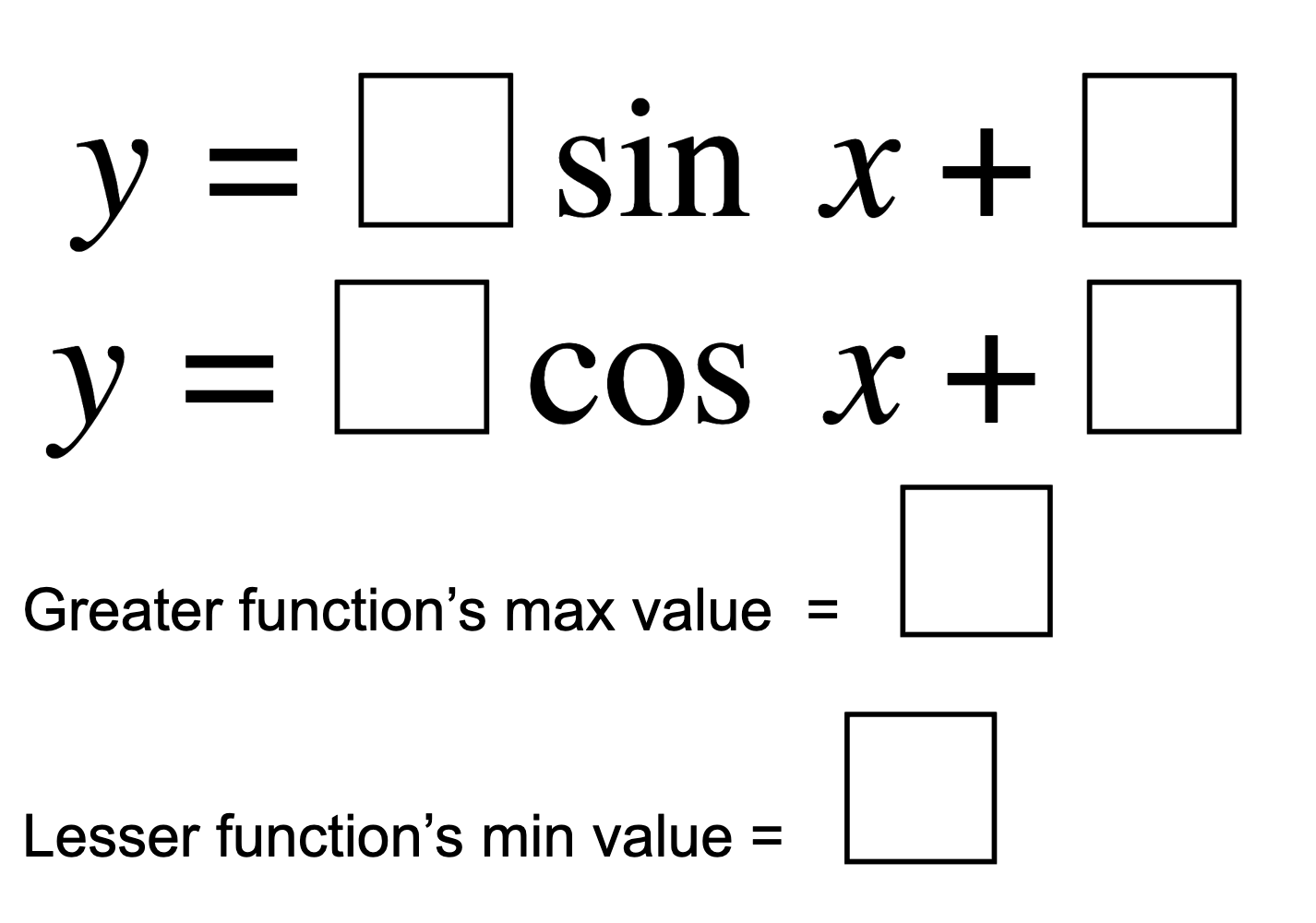
Hint
How does changing the coefficient in front of the sine or cosine term affect its graph? How does changing the constant affect its graph?
Answer
Four solutions have been found so far. Here they are:
y = 1 sin(x) + 4, y = 2 cos(x) + 7, max = 9, min = 3
y = 2 sin(x) + 7, y = 1 cos(x) + 4, max = 9, min = 3
y = 1 sin(x) + 8, y = 2 cos(x) + 5, max = 9, min = 3
y = 2 sin(x) + 5, y = 1 cos(x) + 8, max = 9, min = 3
y = 1 sin(x) + 4, y = 2 cos(x) + 7, max = 9, min = 3
y = 2 sin(x) + 7, y = 1 cos(x) + 4, max = 9, min = 3
y = 1 sin(x) + 8, y = 2 cos(x) + 5, max = 9, min = 3
y = 2 sin(x) + 5, y = 1 cos(x) + 8, max = 9, min = 3
For an interactive version of this problem created in GeoGebra, click here.
Source: Tim Brzezinski
Here are 3 more solutions I came up with for Sine and Cosine Waves:
y = 2 sin(x) + 6, y = 3 cos(x) + 4, max = 8, min = 1
y = 1 sin(x) + 4, y = 3 cos(x) + 5, max = 8, min = 2
y = 4 sin(x) + 5, y = 2 cos(x) + 6, max = 9, min = 1