Open Middle®
Directions: Using the digits 1 to 9, at most one time each, place a digit in each box to find the function’s greatest possible value.
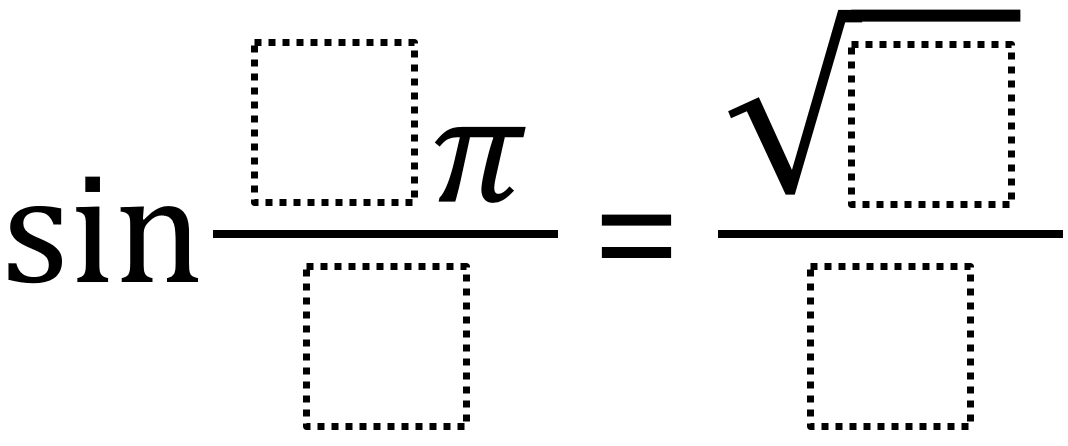
Hint
What values of pi are more likely to result in a larger value?
How can equivalent fractions allow us to avoid using a number more than once?
How can equivalent fractions allow us to avoid using a number more than once?
Answer
Crystal Spellmann found the greatest possible value of 1 by using sin 3π/6=√4/2
Source: Robert Kaplinsky
I used sin 3π/6=√4/2. The largest value for the sine function is 1.
Thanks Crystal! I’ll get this corrected.
Other solutions: sin(1π/2)=√9/3, sin(2π/4)=√9/3. New problem idea using digits 1-9 each at most once (not sure if its here already: sin ( (_)pi/(_)) + (cos (_)pi/(_)) = sqrt()/()