Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make each equation true.
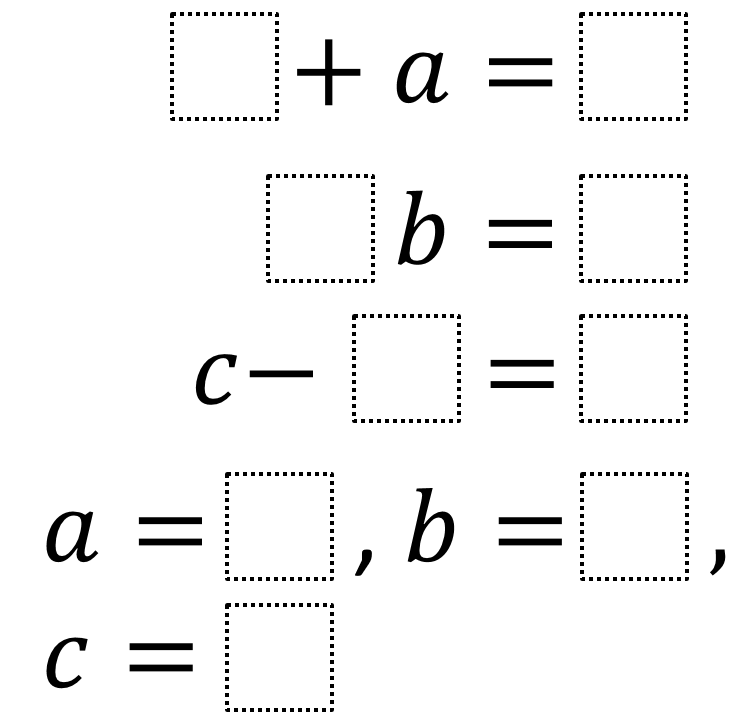
Hint
What is the largest possible value that the coefficient of b can be?
Answer
4 + a = 9
3 * b = 6
c – 7 = 1
a = 5, b = 2, c = 8
Number of Unique Solutions: 16
1: 1 + a = 8, 2b = 6, c – 4 = 5 with a = 7, b = 3, c = 9
2: 1 + a = 8, 2b = 6, c – 5 = 4 with a = 7, b = 3, c = 9
3: 1 + a = 8, 3b = 6, c – 4 = 5 with a = 7, b = 2, c = 9
4: 1 + a = 8, 3b = 6, c – 5 = 4 with a = 7, b = 2, c = 9
5: 4 + a = 9, 2b = 6, c – 1 = 7 with a = 5, b = 3, c = 8
6: 4 + a = 9, 2b = 6, c – 7 = 1 with a = 5, b = 3, c = 8
7: 4 + a = 9, 3b = 6, c – 1 = 7 with a = 5, b = 2, c = 8
8: 4 + a = 9, 3b = 6, c – 7 = 1 with a = 5, b = 2, c = 8
9: 5 + a = 9, 2b = 6, c – 1 = 7 with a = 4, b = 3, c = 8
10: 5 + a = 9, 2b = 6, c – 7 = 1 with a = 4, b = 3, c = 8
11: 5 + a = 9, 3b = 6, c – 1 = 7 with a = 4, b = 2, c = 8
12: 5 + a = 9, 3b = 6, c – 7 = 1 with a = 4, b = 2, c = 8
13: 7 + a = 8, 2b = 6, c – 4 = 5 with a = 1, b = 3, c = 9
14: 7 + a = 8, 2b = 6, c – 5 = 4 with a = 1, b = 3, c = 9
15: 7 + a = 8, 3b = 6, c – 4 = 5 with a = 1, b = 2, c = 9
16: 7 + a = 8, 3b = 6, c – 5 = 4 with a = 1, b = 2, c = 9
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



This answer does not seem to fit the problem (please let me know if I am missing something).
The answer I got was:
4 + a = 9
3 * b = 6
c – 7 = 1
a = 5, b = 2, c = 8
I am using this problem in PD tomorrow, so please let me know if there is an error in my thinking. 🙂
Thanks Barb. I’m not sure how that answer got switched into this problem. I can’t remember what answer I originally got. Your’s definitely works though. Probably others too.
Another student came up with
1+a=8
3b=6
c-4=5
a=7, b=2, c=9
The thought process in this question reminds me of Ken Ken Puzzles. These can be played on-line or you can receive an weekly email with printable puzzles. http://www.kenkenpuzzle.com/teachers/classroom
– I do not work for Ken Ken…just love them.
We, 6th-grade students, (Sivan and Diana) have also found another solution while using our teacher’s practice, it was:
1+a=8
3b=6
C-4=5
A=7
B=2
C=9
There are 8 unique solutions (times 2 because you could swap the two numbers in c – x = y to get another solution):
7 + a = 8; 3 * b = 6; c – 4 = 5; a = 1; b = 2; c = 9
7 + a = 8; 2 * b = 6; c – 4 = 5; a = 1; b = 3; c = 9
5 + a = 9; 3 * b = 6; c – 1 = 7; a = 4; b = 2; c = 8
5 + a = 9; 2 * b = 6; c – 1 = 7; a = 4; b = 3; c = 8
4 + a = 9; 3 * b = 6; c – 1 = 7; a = 5; b = 2; c = 8
4 + a = 9; 2 * b = 6; c – 1 = 7; a = 5; b = 3; c = 8
1 + a = 8; 3 * b = 6; c – 4 = 5; a = 7; b = 2; c = 9
1 + a = 8; 2 * b = 6; c – 4 = 5; a = 7; b = 3; c = 9
Which can be divided by 4 again, because 2 of them are the same as all the others, except that the addends in the first equation or the factors in the second equation are swapped, leaving us with only 2 unique solutions:
7 + a = 8; 3 * b = 6; c – 4 = 5; a = 1; b = 2; c = 9
5 + a = 9; 3 * b = 6; c – 1 = 7; a = 4; b = 2; c = 8