Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make the smallest (or largest) difference.
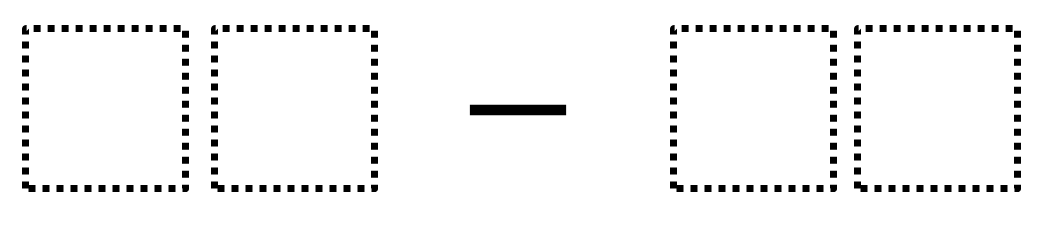
Hint
What does the number on the left represent? What does the number on the right represent?
Answer
98 – 12 is the largest difference. There are several answers for the smallest difference including 81-79.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Wouldn’t 20-19 be the smalls difference? or am I missing a given requirement?
Thanks!
“smallest” I meant. 🙂 Typo!
Sorry…I see what I did wrong! My mistake!
Hi Kim. I think it comes down to the reality that “small” and “large” are not mathematically precise words. I have experimented with using phrasing like “least difference” but that seemed to do more harm than good. So, I have stuck with smallest difference and then wind up having a conversation about what is meant by that.
The problem is a great one! I had just misread it…my mistake. Thanks!
I am finishing your Empowered problem solving workshop and now I am browsing here … I know it’s been a few years since these coments were posted but I wonder if you have tried teaching subtraction/difference refering to it as how far or close are two numbers on a number line?
Sorry, no i haven’t had a chance to try that.
A zero digit was not an option. Only digits 1-9.
I’m doing this now with my 2nd graders and their first question was, “Can we go into the negatives?!” After thinking about this for a moment, I figured that you absolutely could go into the negatives! Is my thinking correct? Here is what they came up with: 12 – 98 = -86 and 97 – 86 = 11. Thanks for stretching our brains!
Your explorations hit at the heart of the challenge between language that feels comfortable to say out loud and language that is mathematically precise. Specifically, what does “smallest difference” mean?
Is -90 a smaller difference than 1? Perhaps “least difference” would be more precise?
Another way to express what I meant by the problem would be to say that if you put the two whole numbers on a number line, then I want the space between them to be the least (or smallest) possible. Where it gets icky is how -86 < 2 but in this context, is a larger difference. Thoughts?
Would it be okay to preface the problem with the statement, Two numbers are on a number line, make the largest or smallest difference between them…
Hi,
Why are there four ADDITION sentences to write down for First try: Second try: etc. ??
For example, if I chose 98-76 = 22 as my first try, wouldn’t I just record it that way? Or is the intention for the student to write: 22 + 76 = 98 ?
A few students and parents believe it to be a typo and that there should be four blank SUBTRACTION sentences for the 1st through 4th tries. THANKS!
My mistake.
I think that one of my colleagues altered the document to include those sentences. I will check with them. So Sorry!
No worries. I was a bit confused.
The largest difference I got was 98 – 12 = 86.
The smallest difference I got was 91 – 87 = 4.
98-12
97-86=11