Directions: Use the digits 1-9 each once to make a the largest possible sum.
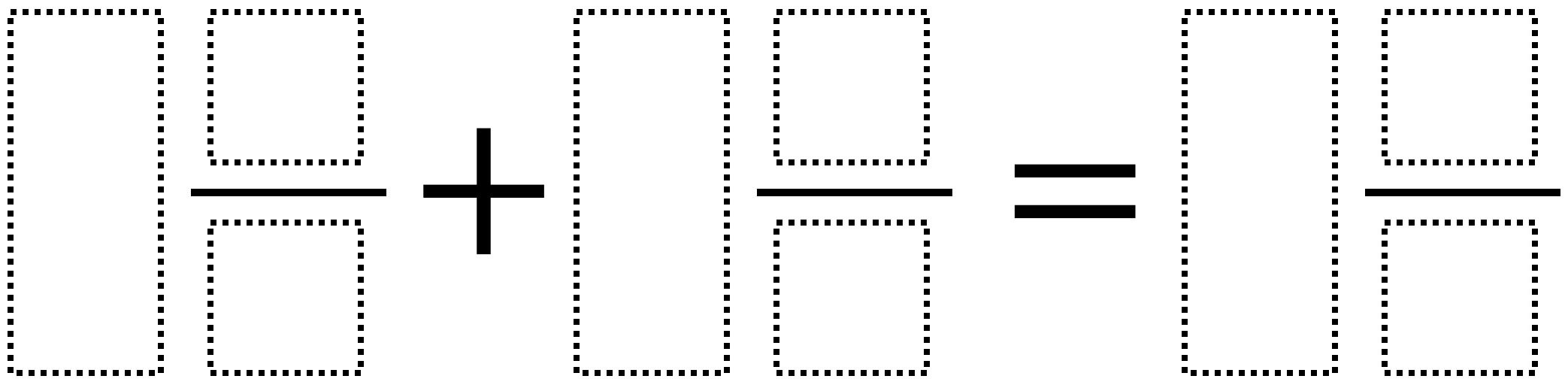
Hint
What assumptions are we making about the fractions we are able to use? Do fractions have to be in lowest terms? How can we figure out if we want the larger numbers to be part of the addends or sum?
Answer
There are many answers in the comments below. One I got was 9 2/4 + 5 3/6 = 7 8/1
Source: Robert Kaplinsky and Ellen Metzger
 Open Middle®
Open Middle®



This was a pretty tough problem. Had my class stumped. I eventually came up with 5 and 6/3 + 4 and 8/2 = 9 and 7/1. 9 and 7/1 = 16.
Thanks for the problem.
Just realized my mistake after looking over my work. 6/3 is only 2, which would result in a total of 15 not 16. Back to the drawing board.
My students found this:
2 4/8 + 7 1/3 = 9 5/6
Without using improper fractions in your mixed numbers. We came up with 9 and 6/7 plus 8 and 4/5 which equals 18 and 23/35
I didn’t realize that the 1 to 9 rule also applied to the answer.
My students said “This problem is so intriguing!”
One of my 5th graders came up with:
5 4/6 + 7 1/3 = 9 8/2
My students found: 7 and 5/2 plus 1 and 3/6 which equals 9 and 8/4. They were pretty excited! I also added that now they needed to find another way, as perhaps a sum of 11 wasn’t the highest sum.
My students found 2 4/8 + 9 3/6 = 7 5/1
2 1/2 + 9 1/2 = 12
Hello. I am a student and was very stumped. But, I figured out that 2 4/8 plus 7 1/3 gets me 9 5/6.
8 6/4 + 5 3/2 = 9 7/1 = 16
12
Well i got 3 14/16 + 2 7/9 = 6 1/6 (simplest form)
9 7/2 +8 6/3= 23 2/6
53 unique solutions. You can always a) swap the whole parts of the two mixed numbers on the left, b) swap the numerators of the whole parts of the two mixed numbers on the left, c) do both swaps a and b, creating 3 additional solutions for each of those 53 unique ones. And then you can swap the addends, doubling the number again, resulting in 53*3*2 = 318 solutions. Here are the 53 unique ones:
1 6/8 + 2 9/3 = 5 7/4 = 6.75
2 1/6 + 5 3/9 = 7 4/8 = 7.5
1 2/8 + 5 9/6 = 7 3/4 = 7.75
1 3/9 + 5 4/2 = 7 8/6 = 8.3333
1 5/2 + 3 8/4 = 7 9/6 = 8.5
3 1/4 + 5 2/8 = 7 9/6 = 8.5
1 2/4 + 7 3/9 = 8 5/6 = 8.8333
1 3/9 + 4 7/2 = 8 5/6 = 8.8333
1 3/2 + 5 9/6 = 7 8/4 = 9.0
1 3/9 + 7 4/6 = 5 8/2 = 9.0
3 1/2 + 5 6/8 = 7 9/4 = 9.25
1 2/3 + 7 5/6 = 9 4/8 = 9.5
1 2/8 + 7 5/4 = 9 3/6 = 9.5
1 3/4 + 7 6/8 = 5 9/2 = 9.5
1 4/8 + 5 9/3 = 6 7/2 = 9.5
2 1/6 + 5 7/3 = 9 4/8 = 9.5
2 1/3 + 7 4/8 = 9 5/6 = 9.8333
1 4/8 + 6 5/2 = 7 9/3 = 10.0
2 6/8 + 5 9/4 = 3 7/1 = 10.0
2 6/8 + 5 9/4 = 7 3/1 = 10.0
1 5/2 + 4 8/3 = 9 7/6 = 10.1667
1 2/8 + 7 6/3 = 9 5/4 = 10.25
1 3/2 + 7 6/8 = 9 5/4 = 10.25
1 4/2 + 5 7/3 = 9 8/6 = 10.3333
1 5/6 + 4 9/2 = 8 7/3 = 10.3333
1 2/4 + 8 7/6 = 9 5/3 = 10.6667
2 3/1 + 5 6/8 = 9 7/4 = 10.75
2 5/1 + 3 6/8 = 9 7/4 = 10.75
3 2/1 + 5 6/8 = 9 7/4 = 10.75
1 3/6 + 7 5/2 = 9 8/4 = 11.0
1 4/8 + 7 5/2 = 9 6/3 = 11.0
1 5/3 + 7 8/6 = 9 4/2 = 11.0
1 6/4 + 5 7/2 = 8 9/3 = 11.0
1 4/3 + 8 7/6 = 9 5/2 = 11.5
2 3/6 + 9 4/8 = 5 7/1 = 12.0
2 3/6 + 9 4/8 = 7 5/1 = 12.0
2 4/3 + 8 6/9 = 5 7/1 = 12.0
2 4/3 + 8 6/9 = 7 5/1 = 12.0
3 4/8 + 5 9/2 = 6 7/1 = 13.0
3 4/8 + 5 9/2 = 7 6/1 = 13.0
5 1/3 + 7 4/6 = 9 8/2 = 13.0
4 2/6 + 7 8/3 = 5 9/1 = 14.0
4 2/6 + 7 8/3 = 9 5/1 = 14.0
6 2/8 + 7 3/4 = 5 9/1 = 14.0
6 2/8 + 7 3/4 = 9 5/1 = 14.0
4 2/6 + 9 5/3 = 7 8/1 = 15.0
4 2/6 + 9 5/3 = 8 7/1 = 15.0
4 6/2 + 5 9/3 = 7 8/1 = 15.0
4 6/2 + 5 9/3 = 8 7/1 = 15.0
5 2/4 + 9 3/6 = 7 8/1 = 15.0
5 2/4 + 9 3/6 = 8 7/1 = 15.0
5 3/2 + 8 6/4 = 7 9/1 = 16.0
5 3/2 + 8 6/4 = 9 7/1 = 16.0
The largest possible sum, as you can see, is 16 = 5 3/2 + 8 6/4 = 7 9/1 = 9 7/1
However, if you don’t allow improper fractions in the fractional parts of the mixed numbers, then the only solutions are:
1 2/3 + 7 5/6 = 9 4/8 = 9.5
1 2/4 + 7 3/9 = 8 5/6 = 8.8333
2 1/3 + 7 4/8 = 9 5/6 = 9.8333 and
2 1/6 + 5 3/9 = 7 4/8 = 7.5,
making 1 2/3 + 7 5/6 = 9 4/8 = 9.5 the greatest possible sum.
Correction on the last line: Of course, 2 1/3 + 7 4/8 = 9 5/6 = 9.8333 would be the greatest possible sum.
Correction: in b) I mean swap the fractions of the two mixed numbers on the left
9 6/2 + 8 7/3 = 22 1/3
The largest one I came up with was:
9 1/2+6 3/4=16 1/4
9 2/4 + 5 3/6 = 7 8/1
ignore pls 9 6/7 7 4/5= 18 23/25
9 8/2 + 7 6/3 = 22
9 6/7 7 4/5= 18 23/25
8 9/1 + 7 6/2
I came up with 12 23/72
9 1/2 + 8 3/4= 18 1/4
9 7/8 + 5 4/3
9 8/1 + 6 7/2
9 2/4 + 5 3/6 = 7 8/1
BRO THIS IS FRICKING SHIT
9 6/7 + 8 4/5= 18 23/35
9 6/7 + 84/5 18 23/35
9 3/4 + 8 1/2 = 18 1/4
9 6/7 8 4/5 = 18 23/35
5 3/2+8 6/4 = 9 7/1=16