Directions: Use the digits 1 to 9, at most one time each, to fill in the boxes and make a positive and a negative solution.
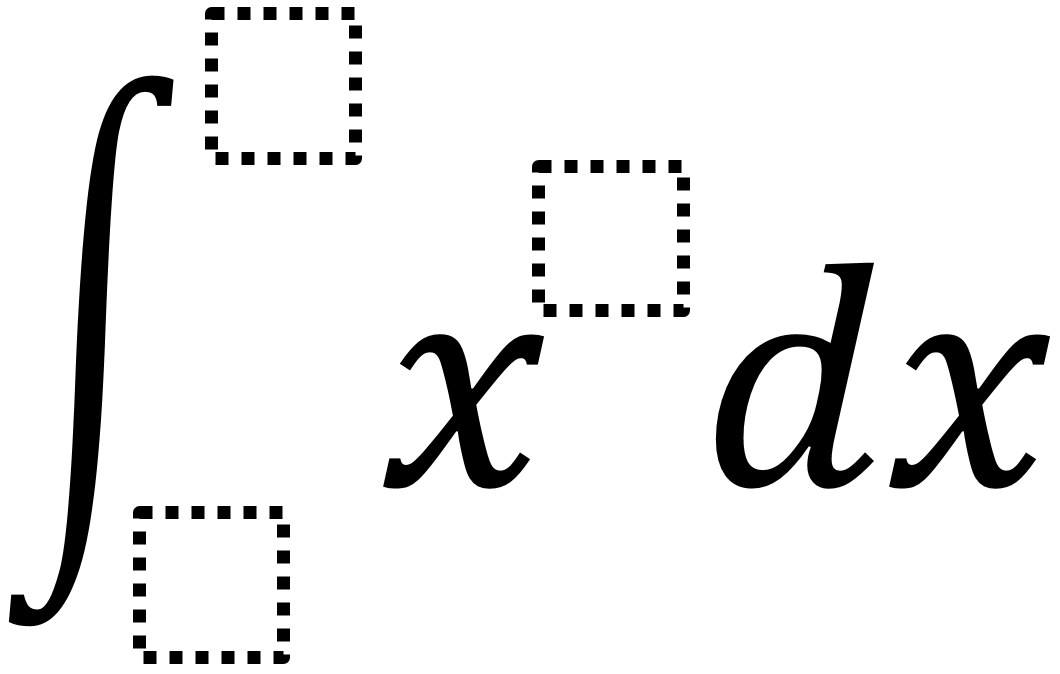
Hint
How does the value of the x’s exponent affect the solution?
How does the placement of the digits in the upper and lower bounds affect whether the solution is positive or negative?
How does the placement of the digits in the upper and lower bounds affect whether the solution is positive or negative?
Answer
There are many answers. It does not matter what the value of the exponent is. The upper and lower bounds can then be any digits as long as they are not replicated. If the upper bound is larger than the lower bound, it will have a positive solution. If the lower bound is larger than the upper bound, it will have a negative solution.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Question regarding this solution. In completion of a definite integral, by definition we are to integrate based on the right bound then the left bound and take the difference of the two values. Given that the missing values of the integral were required to be positive we would need to substitute our definite integral [Left,Right] values in with the smallest value at the base of the integral and the largest value at the top of the integral. With that in mind all integral values would be positive (as well as the function) and we are finding the area under the curve in the first quadrant to the x axis. Why would we violate the definite integral rule to perform this task in order to find a value which we can only find through a rule violation? If I am looking at this incorrectly or misunderstanding a rule, please let me know.
I’m not sure I fully understand your question, Seth. To some degree, we want conversations about what is and is not allowed/possible to come out during the problem solving.