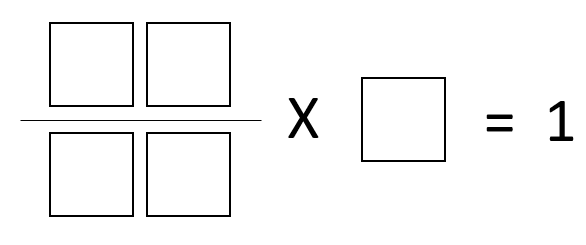
Directions: Using the digits 1 through 9 fill in the blanks to make a product of 1.
Hint
How can you use equivalent fractions?
Answer
Number of Unique Solutions: 22
1: 12 / 84 x 7 = 1
2: 12 / 96 x 8 = 1
3: 13 / 52 x 4 = 1
4: 13 / 78 x 6 = 1
5: 14 / 98 x 7 = 1
6: 16 / 48 x 3 = 1
7: 17 / 34 x 2 = 1
8: 17 / 68 x 4 = 1
9: 18 / 36 x 2 = 1
10: 18 / 54 x 3 = 1
11: 18 / 72 x 4 = 1
12: 19 / 38 x 2 = 1
13: 19 / 57 x 3 = 1
14: 19 / 76 x 4 = 1
15: 26 / 78 x 3 = 1
16: 27 / 81 x 3 = 1
17: 29 / 87 x 3 = 1
18: 34 / 68 x 2 = 1
19: 38 / 76 x 2 = 1
20: 39 / 78 x 2 = 1
21: 43 / 86 x 2 = 1
22: 48 / 96 x 2 = 1
Source: Owen Kaplinsky
 Open Middle®
Open Middle®



The fill in the blanks picture is missing.
Fixed as well.
This was a great task for my class today! I removed the ‘x’ operator and replaced it with ‘of’ to allow space for mental math as we haven’t spent time on the algorithm (yet). As students worked through the problem they asked about using 0, and I agreed they could. They asked about repeating digits, and I agreed. However with each shift they I asked students to tell me WHY that shift might help them, or how would something previous they’d done help them now (if they were making a change). After groups found multiple solutions, we also adapted the question to include finding products other than 1. Our last extension was to include the use of two digit numbers in the original blank for the one digit multiplicand. So many solution possibilities, so many connections to equivalent fractions, and during our consolidation phase, students noticing how the simplest form denominator and the multiplicand were connected. Definitely using this task again!
One of my brilliant 5th graders came up with this answer 21,612/64,836 x 3 = 1
Are you able to repeat digits in the equation or is it using the digits 1-9, only one time for each digit? Also, could it be using the digits 0-9? Thanks!