Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make the smallest (or largest) product.
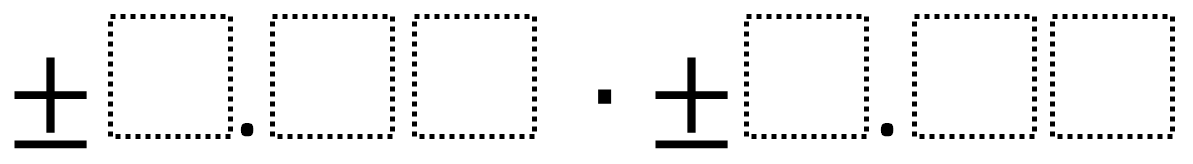
Hint
What number does each box represent?
Answer
SS found the current smallest product with positive factors: 1.35 * 2.46. Kevin Crowl suggested 9.75 * 8.64 which led to 9.64 * 8.75 which is currently the largest product with positive factors. We are still looking for answers. If you have one, post it in the comments.
Note: This problem’s difficulty can be adjusted by altering the number of digits (boxes), picking smallest or largest, or by picking either a positive, negative, or both.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



1.35 * 2.46 ?? smallest for both positive??
Thank you for that solution, it has been added to the problem.
I think largest both positive is 9.75 * 8.64
Thanks Kevin. Challenging, right?! Your solution reminded me how this is similar to another problem. https://www.openmiddle.com/rectangles-maximizing-area/. In this problem, you get the largest area when the side lengths are as close to the same amount as possible. Using that reasoning, I realized that 9.64 * 8.75 is a bit closer together and gives 84.35 as an answer as opposed to 84.24.
Might still be even larger ones!
As I was checking through my students’ work the other day, one of them had also found 9.64*8.75 as the largest possible. I appreciate the confirmation, and my whole class was very excited to hear that one of them had done “better” than me!
Excellent. That kid will remember that for the rest of his life. Those are good moments to have.
Wouldn’t the smallest value then be +9.64 * -8.75 ? Or -9.64 * +8.75 ? The negative value of the largest positive solution?
Does the +- in front of both confuse this problem?
For +_._ _ * –_._ _
Greatest result: 2.46 * –1.35
Smallest result: 9.64 * –7.85
For +_._ _ * +_._ _
Greatest result: 9.64 * 7.85
Smallest result: 2.46 * 1.35
For – _._ _ * –_._ _
Greatest result: –9.64 * –7.85
Smallest result: –2.46 * –1.35
For – _._ _ * +_._ _
Greatest result: –2.46 * 1.35
Smallest result: –9.64 * 7.85
Overall:
Smallest result: –9.64 * 7.85 = 9.64 * –7.85
Smallest positive result: 2.46 * 1.35 = –2.46 * –1.35
Greatest negative result: –2.46 * 1.35 = 2.46 * –1.35
Greatest result: 9.64 * 7.85 = –9.64 * –7.85
Oops, I swapped all the 7s and 8s on accident. Here’s the corrected version:
For +_._ _ * –_._ _
Greatest result: 2.46 * –1.35
Smallest result: 9.64 * –8.75
For +_._ _ * +_._ _
Greatest result: 9.64 * 8.75
Smallest result: 2.46 * 1.35
For – _._ _ * –_._ _
Greatest result: –9.64 * –8.75
Smallest result: –2.46 * –1.35
For – _._ _ * +_._ _
Greatest result: –2.46 * 1.35
Smallest result: –9.64 * 8.75
Overall:
Smallest result: –9.64 * 8.75 = 9.64 * –8.75
Smallest positive result: 2.46 * 1.35 = –2.46 * –1.35
Greatest negative result: –2.46 * 1.35 = 2.46 * –1.35
Greatest result: 9.64 * 8.75 = –9.64 * –8.75
And there can be no better solutions because the whole numbers always have to be as big as possible for the greatest product (so they have to be 8 and 9), then the tenths have to be the second-largest digits (so 6 and 7, where 7 should be multiplied with 9.xx for the greatest possible result, so it goes after the 8) and the hundreths have the least influence, so they should be the largest digits still left (so 4 and 5, where 5 should be multiplied with 9.xx for the greatest possible result, so the 5 goes after 8.7). Same goes for the smallest product: The wholes have to be as small as possible (1 and 2), the tenths should be the second smallest digits (3 and 4) and the hundreths should be the smallest digits still left (5 and 6).
I love adamatitters