Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make the smallest (or largest) quotient.
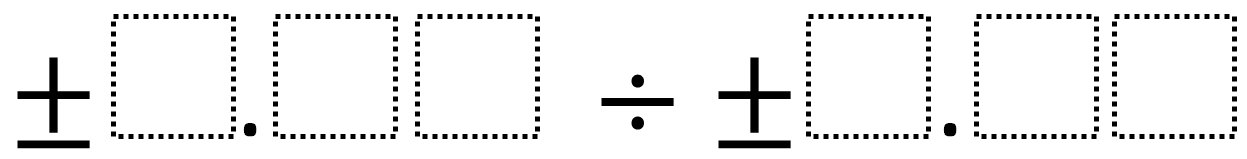
Hint
What number does each box represent?
Answer
No answers yet. If you have one, post it in the comments.
Note: This problem’s difficulty can be adjusted by altering the number of digits (boxes), picking smallest or largest, or by picking either a positive, negative, or both.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Might it be useful to model this graphically with desmos or perhaps wolfram alpha? I’ll work on something this week.
Should probably read “Quotient” instead of sum?
Yep. Good catch. Too much copy and pasting.
I feel that making a small change to find the quotient closest to 1 would add so much more opportunities for students to explore, discuss, and debate. Currently, most will try the smallest possible number (1.23) and divide it by the largest possible number (9.87) and in this case it would work, and switching the order of those 2 numbers would satisfy the prompt of finding the largest quotient. However, if they were trying to find the quotient closest to 1 there are many more combinations to try and better conversations will surface. What does it mean when the quotient is 1, and how can I get as close to that as possible with these constraints? Does the order matter?
For +_._ _ ÷ –_._ _
Greatest result: 9.87 ÷ –6.54
Smallest result: 9.87 ÷ –1.23
For +_._ _ ÷ +_._ _
Greatest result: 9.87 ÷ 1.23
Smallest result: 9.87 ÷ 6.54
For – _._ _ ÷ –_._ _
Greatest result: –9.87 ÷ –1.23
Smallest result: –9.87 ÷ –6.54
For – _._ _ ÷ +_._ _
Greatest result: –9.87 ÷ +6.54
Smallest result: –9.87 ÷ +1.23
Overall:
Smallest result: –9.87 ÷ +1.23 = +9.87 ÷ –1.23
Smallest positive result: 9.87 ÷ 6.54 = –9.87 ÷ –6.54
Greatest negative result: 9.87 ÷ –6.54 = –9.87 ÷ 6.54
Greatest result: 9.87 ÷ 1.23 = –9.87 ÷ –1.23
Greatest result: 9.64 ÷ 8.75
Correction, that is the smallest positive result or could be the greatest negative result.