Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make the smallest (or largest) difference.
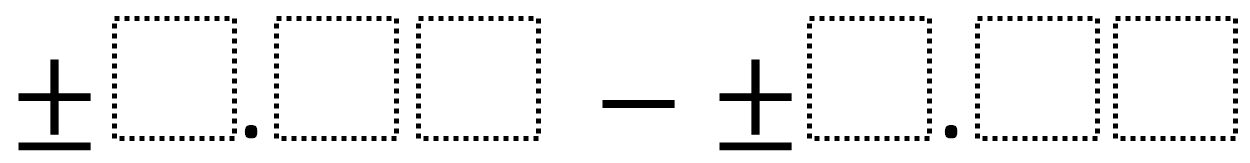
Hint
What number does each box represent?
Answer
No answers yet. If you have one, post it in the comments.
Note: This problem’s difficulty can be adjusted by altering the number of digits (boxes), picking smallest or largest, or by picking either a positive, negative, or both.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Subtracting decimals with integers (positive & negative) is not a 6th grade standard. That’s 7th grade.
Thanks for catching this Kristen. I’ll add 7.NS.1 to the problem.
Just considering positive number answers, using only a positive subtrahend and minuend for 6th grade, the greatest difference would be 8.64, obtained by taking the greatest possible positive number 9.87 and decreasing it by the smallest possible positive number, 1.23. Using only positive numbers again, the smallest possible difference would be 0.14 obtained by creating a mixed number with the greatest possible decimal value .98 and and subtracting it from a number whose ones place number is only 1 greater and whose decimal value is the smallest possible value .12. The possible subtrahend / minuend expressions woukd be: 7.12-6.98, 6.12-5.98, 5.12-4.98, and 4.12-3.98.
When having my 7th graders decide what integer sign to use the least value they could find was -9.65 – 8.74 = -18.39 or -9.75 – 8.64 = -18.39.
For +_._ _ – –_._ _
Greatest result: +9.75 – –8.64 = 18.39
Smallest result: +2.46 – –1.35 = 3.81
For +_._ _ – +_._ _
Greatest result: +9.87 – +1.23 = 8.64
Smallest positive result: +7.12 – +6.98 = 0.14
Greatest positive result: +6.98 – +7.12 = –0.14
Smallest result: +1.23 – +9.87 = –8.64
For – _._ _ – –_._ _
Greatest result: –1.23 – –9.87 = 8.64
Smallest positive result: –6.98 – –7.12 = 0.14
Greatest positive result: –7.12 – –6.98 = –0.14
Smallest result: –9.87 – –1.23 = –8.64
For – _._ _ – +_._ _
Greatest result: –2.46 – +1.35 = –3.81
Smallest result: –9.75 – +8.64 = –18.39
Overall:
Smallest result: –9.75 – +8.64 = –18.39
Smallest positive result: –6.98 – –7.12 = 0.14
Greatest positive result: –7.12 – –6.98 = –0.14
Greatest result: +9.75 – –8.64 = +18.39
It’s really equivalent to the exercise “Adding Decimals (Middle School)” (https://www.openmiddle.com/adding-decimals-middle-school/). Which makes it strange that that one has the tag 5.NBT.6, while this one has the tag 7.NS.1
Oops, I made a mistake. “Greatest positive result” should really be “Greatest negative result” (meaning the negative result closest to 0)