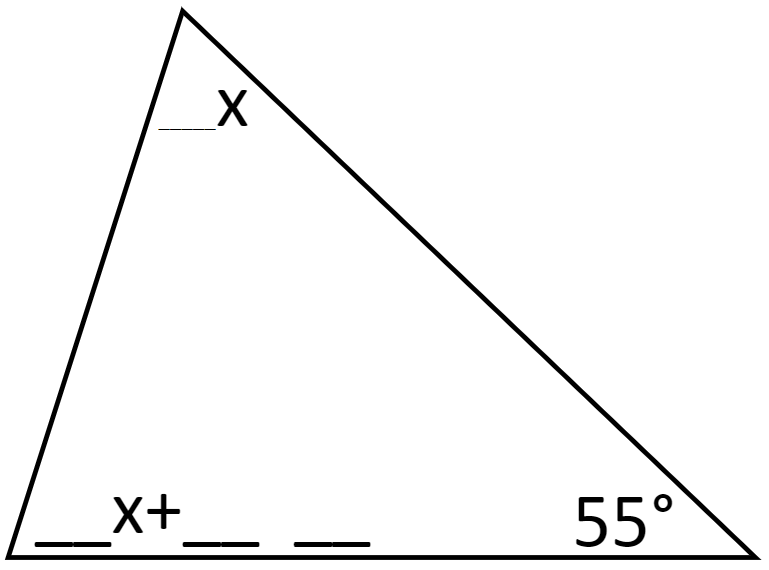
Directions: Using the digits 1-9 at most one time each, fill in the blanks so that when you solve for x, it is a whole number.
Hint
How many degrees must the two unknown angles sum to?
Can you write an equation to represent the sum of the two unknown angles?
Can you write an equation to represent the sum of the two unknown angles?
Answer
There are many answers. One is:
Top angle is 4x and bottom angle is 6x + 25.
x = 10 solves the problem.
Top angle is 4x and bottom angle is 6x + 25.
x = 10 solves the problem.
Extension/extra challenge 1: set a value for x and find all the ways to make the problem have that solution.
Extension/extra challenge 2: change the value of the bottom right angle.
Source: Franco D. Adkins
 Open Middle®
Open Middle®



This makes sense for the most part
This kind of makes sense
I understand it
How?
I get it a little still a little confusing.
It’s a little confusing, but for the most part I get it
Can someone explain
The two unknown angles must add up to 125. That is what we know from the triangular theorem, that the sum of all angles must be 180 degrees; thus if we begin with 55, the remainder is 125.
Any two whole numbers adding up to 125 would be OK, only, one is represented ’_x+__’, which means that there is a double digit number next to the ’x part’.
If we try to use too large or small numbers for our x, we cannot get double digits.
63+62=125 could come from x=9, ie 7x+(6x+8) but 8 is only one digit.
Also, many examples could leave us with no extra number:
100+25=125 could have been ok but that addition could mean x=25 and 4x+x=125 and no extra number.
But try 50+75 and use x=10:
50+75=125 and then 5x+(6x+15), which is ok!
[We have to think of 75 as being 6x+15 even though it could also be written as 7x+5, but then we see a single digit again and that is not ok.]
Has anyone tried this with their kids? I would love to know how the lesson went!
Cool thing about open middle is to just try it and you will see the students come up with ideas/solutions that you would never even think about. I have my students come up to dry erase boards in groups around the whole classroom, all at once. This allows me to see all the “discussions” taking place – some students are trying to figure it out and arguing with each other, some groups the “A” student is explaining to others how its done and helping them see what happens when you change one of the digits. All of these discussions reinforces the basic concept of the problem.
My 6 eighth graders enjoyed this!